Refresher on Research Methods

Kevin R Foster, CCNY

Fall 2012

 

 

 

Topics include:

1.       Basics about CCNY, MA program, and keeping current here

2.      Plagiarism and rules for proper citations

3.       Internet searches and databases (EconLit, JStor, Lexis/Nexus)

4.      Sources of data for economics

5.      Basics of computers: MS Word & Excel (including equation editor and Analysis ToolPak)

6.      Math Review (percentage growth, exponents, ex and ln(x))

7.       Crash lesson on derivatives ("double the coefficient rule")

 

Below are some (random) thoughts on each one.  Note that this online version is an ongoing draft  check periodically to get the latest version.  This is a draft, so please be generous in sending suggestions, corrections, or errata to kfoster@ccny.cuny.edu.

 

 

 

Don't just print out the whole pdf file, please  that's a waste of paper!

 

 

 

1. Basics

 

Welcome to the CCNY MA Economics program!  I have a few items here to give advice to new students.  Please excuse me if they are too basic, but I want to make sure that everyone knows about these.

 

  1. Keep in touch!  The MA advisor for Economics is Prof. Matt Nagler.  You've probably already talked with him and/or me, and you should keep in regular contact.  If you have any problems, speak with one of us first.  Don't wait; don't try to hide and hope the problem goes away.  We will try to help you out
     or at least give you an idea about what options are available to you.  (Of course you can also talk with any of the other faculty & staff here.)  The worst problems for students here come about when someone spends 6 or 8 weeks hiding, hoping that their problem will go away, not realizing that they've dug themselves into a deep hole from all of the waiting!
  2. On the same topic of keeping in touch
     activate your CCNY Email Account!  You can set it to auto-forward to another account (gmail, yahoo, whatever…) if you read that one more often.  You will get updates from me and from other faculty sent out to the CCNY email address.  You'll also get registration information.  If you don't check it often enough, you will miss out.
  3. The CCNY email links to the "Blackboard" course webpage, which you access through the CUNY Portal (my webpage has a link as does the college web page). 
  4. We also use InYourClass.com so login there to chat with the class.
  5. Form and work with a study group.  You will learn more from your fellow students than from any faculty member.  Numerous studies have shown that students working in teams learn more and do better on exams.

 

 

2. Plagiarism

Read CUNY's policy on acadmic integrity (on the course syllabus and CCNY web page).

see also http://www.dartmouth.edu/~sources/, http://www.princeton.edu/pr/pub/integrity/index.html http://www.economics.harvard.edu/files/WritingEconomics.pdf

RULES:

example of cite:

          "The full time earnings of black and Hispanic women averaged less than 60 percent of white male earnings" (Ehrenberg and Smith, p. 417).

example of long quote with cite:

Word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word word (BlabBlab, p. 10000)

example:

          In 1997, Hispanic females earned 51% of what White males earned (Ehrenberg and Smith, p. 417).

examples:

Ehrenberg, Ronald G., and Robert S. Smith, (2000). Modern Labor Economics: Theory and Policy, seventh edition. New York: Addison-Wesley.

Heckman, James, (1974). "Shadow Prices, Market Wages, and Labor Supply," Econometrica, 42(4).

Bureau of Labor Statistics, (2000). Data on "1998 Internet and Computer Use," downloaded from http://www.bls.census.gov/cps/computer/1998/sdata.htm

Vames, Steven, (2000). "Income Gains in March Outpaced Spending," New York Times Online, April 28, 2000. http://www.nytimes.com/yr/mo/day/news/financial/28tsc-economy.html

CONSEQUENCES

Failure to follow these rules is a violation of Academic Integrity.  This is a severe violation of the basic principles of the academic community.  You may be brought up on academic charges before a Disciplinary Committee of the College, where you are subject to a range of consequences up to expulsion.

 

 

3. Internet Resources

 

An internet search on a given topic will return a wide variety of hits.  The most difficult task is to differentiate the junk (most of it) from the few bits of useful information.  Since you are a student, just beginning to learn the field, it is only to be expected that you will have a more difficult time distinguishing the good from the bad.  You must be wise, dutiful in checking out sources, and should ask questions.

 

You might usefully create a web page of your own.  This takes about 30 minutes to learn, and removes any mystery.  Some students still think that publishing online is difficult, so only very high-quality material should be online  FALSE.  Any imbecile can put any damn thing online  and we do!  You've got to be careful.  Blogs and wikis have lowered the bar even further.  A reader needs to be careful and critical of every source.

 

There are certain sources that have filtered out much of the worst junk.  You can limit your search to only articles published in refereed journals by searching online databases (from the CCNY Library), such as EconLit and JStor.  Of course not everything that is published is correct  you must still be diligent in finding recent sources, making your own evaluation of the plausibility of the claims, and arriving at your own judgments.

 

Both of these links are easily found from the CCNY Library's page, where you can pick them from the list.  You need to access them from a CCNY computer, or else you will need a login (which the library can provide you, however this takes time so don't wait for the night before the paper is due!)

 

EconLit collects citations, most with a detailed abstract, and a large fraction have full text available.  "Full text" means that you don't have to find the physical journal; you never touch paper.  Just save the .pdf file that it produces.  Sometimes there is no linked fulltext but a Google search of author/title will hit.

 

A hint: one of my favorite journals to recommend to students is the Journal of Economic Perspectives (JEP).  This gives excellent overviews of particular topics in economics, meant to be accessible to a non-specialist, written by some of the most prominent people in those fields.  It is published by the American Economic Association (AEA) and is available through both EconLit and JStor.  The Journal of Economic Literature (JEL) if also from the AEA and it also has occasional articles that summarize a topic.  The library has both journals on the shelves  you can browse through these journals, just skimming to find interesting articles.  It's a great way to spend a few hours!

 

JStor has the full text of articles published in the foremost journals of various disciplines (including Economics, Finance, and Statistics).  Generally these articles are at least 3-5 years old, but it gives access to every article in the most important journals for the past several decades.

 

For news stories, you can search Lexis/Nexus.  This collects the full text of major newspapers, including the New York Times and the Economist.  Again, you need to access them from a CCNY computer, or get a login to work remotely.

 

There are other outlets, such as prominent and well-regarded thinktanks and policy institutions.  In economics, the National Bureau of Economic Research (NBER, at www.nber.org) is highly regarded, as is the Brookings Institution (www.brookings.edu).

 

Of course all of these sources give "the establishment view" not the ideas and opinions of extremists.  This is true by definition: formerly extreme views become mainstream once "the establishment" has published them.  I do not want to discourage you from research on the fringes, however many classes at this College will require that you demonstrate a knowledge of the mainstream.  (Marx and Keynes began their radical writings by first demonstrating their knowledge of what had been written previously, to show where it had holes.)

 

 

Finally, the CUNY library catalog is CUNY+.  I often find it useful to click on the tab for "Select Individual CUNY Libraries" to search only CCNY's library.  Then, if this one doesn't have it, you can search the other CUNY schools.

 

 

4. Sources of data for economics

There are many sources of econmics data online.  Although the principal sources change depending on the field, here are some of the basics:

http://rfe.org  RFE is Resources for Economists, sponsored by the American Economic Association.  It is a great site, a clearinghouse for all of the important econ sites.

http://www.federalreserve.gov  The Federal Reserve

http://www.ny.frb.org  our own New York Fed

http://www.census.gov/ the US Census

          [or http://www.census.gov/main/www/subjects.html is a list of topics on which the Census Bureau has data.]

http://stats.bls.gov/ is the Bureau of Labor Statistics

http://www.oswego.edu/~economic/data.htm is a good portmanteau of links from SUNY Oswego

http://www.worldbank.org/lsms/ World Bank

 

CPI  www.bls.gov/cpi/home.htm

CPI Chained http://www.bls.gov/cpi/super_cpi.pdf

PPI www.bls.gov/ppi/home.htm

Overview of BLS data www.bls.gov/bls/inflation.htm

GDP Deflator (from BEA) www.bea.gov/bea/dn/home/gdp.htm

Overview of BEA data http://www.bea.gov/

GDP www.bea.gov/bea/dn/home/gdp.htm

NIPA tables www.bea.gov/bea/dn/home/gdp.htm

Unemployment www.bls.gov/cps/home.htm

Wages www.bls.gov/bls/employment.htm

BLS details on coverage www.bls.gov/opub/hom/homch1_a.htm

 

 

 

5. Basics of computers: MS Word & Excel (including equation editor and Analysis ToolPak)

 

Scary basic...

 

You will be using a few computer programs a lot while you're in college.  The most common programs that an econ student would use are:

-          an internet browser, like Microsoft's Internet Explorer or Mozilla's Firefox or Google Chrome or Apple Safari or Opera or ....

-          a word processing program, probably Microsoft Word although OpenOffice gives a free version

-          a spreadsheet, probably Microsoft Excel although OpenOffice gives a free version

-          a presentation program, such as Microsoft PowerPoint or OpenOffice version

-          data analysis programs such as SAS or SPSS (for econometrics)

-          mathematical programs such as Matlab or Gauss (for advanced work)

 

I recommend OpenOffice to you, especially if you have a little netbook.  It does most everything that you would pay Microsoft for but it's free.

 

The internet browser is one of the most basic, which you've used if you've ever read a web page.  In the Econ computer lab, just double click (click the left-hand button on the mouse twice in quick succession) when the arrow (moved by the mouse) is on the picture above the words "Internet Explorer."  From there you can click to find the world!

 

The word processor is what you'll use to write papers.  You basically just type the text that you want.  It has a few extras, for instance you can click on "Insert" (on the bar on top) and choose to insert pictures (if you have them on disk) or charts from a stats program.  The other common thing to insert is an equation.  Getting to the equation editor requires going to "Insert" then "Object…" then find "Microsoft Equation" under the "Create New" tab.  Equation Editor is useful to produce text such as:

           

or whatever ferocious-looking stuff you want to create.  Read the Help section to figure out all of the details of how to create equations with subscripts, superscripts, sum and integral signs with the proper notations, etc.

 

The more practice you have with MS Word, the better you'll get, using things like bold, italics, sub- or super- scripts, new fonts,  tables, pictures, graphs, etc.  You can get tips from other students, who were once as new to computing as you are now!  There's no shame in not knowing something; the shame is to choose to remain ignorant.

 

If you go to "File" then "New" you can find templates for common document types: they have some decent resume templates, for instance.  Of course if you're a professional graphic designer you can do better, but if you're a novice you can do worse!

 

The next common MS program is Excel, for spreadsheets.  This is just a fancy calculator that can do a great deal of work for you.  You might use it in many classes.  Suppose you have data on some statistic that x = 100, 110, 121, 133.  You type those four values into the spreadsheet like this:

100

110

121

133

Suppose you want to find the percent growth.  The formula for percent growth from x0 to x1 is .  So in the next column we want to type a formula to find this growth rate.  The first row we leave blank, but the next row we type the equals sign, "=", which tells the program that you're entering a formula.

100

 

110

=

121

 

133

 

Then after typing the equal sign (but before hitting return or some other key) we can just click to reference any other value.  We want to find the difference so we click on the cell where we typed "110" then the minus key, "-", then click on the cell where we have 100.  Note that Excel will fill in its version of the formula: if you typed the numbers in column A and the formula in column B, then the formula in the second row of column B (which is B2) will read "=A2-A1" which tells Excel to subtract the value in A1 from the value in A2.  It will look like:

100

 

110

=A2-A1

120

 

130

 

Now hit enter and Excel will calculate the value.  Next you can then copy the formula (click on the cell with the formula you want then "Edit/Copy") and paste it in to the other cells, getting:

100

 

110

10

121

11

133

12

For only four numbers that's not a big time-saving but you can imagine if you have, say, quarterly data on GDP back to 1948.  To find the percent change we next take the difference and divide by the initial value, so in the second row of column C we type "=" again, then click on the cell with 10 then the divide "/" then click on the cell with 100.  Now Excel creates the formula "=B2/A1", or 0.1.  Copy this down so get:

100

 

 

110

10

0.1

121

11

0.1

133

12

0.099174

If you forget how to convert decimals to percents you just highlight the cells in column C that you want to format, click on the "%" button, and Excel does it for you. 

 

Of course you would have done the calculation in one step by entering the formula (in D2) as "=(A2-A1)/A1". 

 

You will quickly figure out that you can write much more complicated formulas, which can use Excel's embedded formulas: from simple ones like "=sqrt(A2)" to ln(A3) to particular Excel formulas (check the Help menu or the button marked  to see a list) for stats like Average, financial formulas for annuities or time value of money problems, even some that you probably haven't heard of.

 

Excel will plot figures ("Insert" then "Chart" to see the many types) and do basic data analysis ("Tools" then "Data Analysis" for regressions, histograms, lots of the basics).  You can use it to present and analyze small datasets.  (Where "small" is hard-coded into older versions of the program to mean less than about 65,000 observations.)  Macro data is often short enough to fit (even monthly data on, say, industrial production, is available for maybe 70 years so that's just 840 obs!) while many other datasets are far larger.

 

But note that you must have the "Analysis TookPak" installed, if you're using Excel at home.  For Excel 2003 you can just find "Add-in's" and follow those instructions; for other versions you should just search under the Help menu for Analysis TookPak (note the strange spelling  another reason to condemn Bill Gates).

 

 

 

6. Math Review (percentage growth, exponents, exp and ln(x))

 

Percent:

Remember that a percent is just a convenient way of writing a decimal. So 15% is really the number 0.15, 99% is 0.99, and 150% is 1.50. I assume you know this, but sometimes it can get confusing. For instance, we might want to find 10% of 10%. We CANNOT just multiply 10*10, get 100, and leave that as the answer! Rather we first convert them to decimals and then multiply: so 0.10 * 0.10 = 0.01 = 1%.

Examples: (click on the ? to get the answers).

30%*7% + 70%*5% = ?

50%*10% + 50%*3% = ?

Percentage Change (Growth Rate):

Consider GDP in the Great Depression. The data (billions of $) are:

1929

103.8

1930

91.1

1931

76.4

1932

58.6

1933

56.2

We want to figure out the percentage change in GDP during the Depression. We can see that, from 1929 to 1930, US GDP fell by $(103.8 - 91.1) bn = $12.7 bn. But how big is this? From the first to the second quarter of 1997, US GDP grew by $108.4 bn (from 7955 to 8063.4). The economy has gotten much larger in the intervening span of time. The percentage change in GDP tells us how large the fall in GDP was, relative to the total amount of $103.8bn available to be lost.

So we calculate the percentage change in GDP as (91.1 - 103.8)/103.8, which is -0.1223. To make this decimal into a percentage, we multiply by 100 (move the decimal point 2 spots to the right), so this is a growth rate of -12.23% (or a fall of 12.23% -- sometimes we use a word instead of the negative sign). In general, if we have values for some series, x, and write x1, x2, x3, ... (where the subscript number refers to the time period) the percent change from time 1 to time 2 is 100 * . We also sometimes write this as the change in x (  ) divided by the level of x, or 100* . Finally, we can also calculate the percentage change as 100*  which is the same thing (as a bit of algebra should be able to convince you).

Examples:

What are the percent changes for US GDP in the years of the Great Depression? Answer.

Calculus and Percentages:

Calculus (for those of you who have taken the course) can simplify our use of percentages and percentage changes. Remember that the derivative gives us the change in the value, so . Then remember that the derivative of the natural logarithm is , which is the formula for the percent change. Thus the derivative of the natural log is the percentage change (another reason that logarithms are your friend!).

 

  

 

 

 

Answers:

Percent:

30%*7% + 70%*5% = 0.3*0.07 + 0.7+0.05 = 0.021 + 0.035 = 0.056 = 5.6%

50%*10% + 50%*3% = 0.5*0.1 + 0.5*0.03 = 0.05 + 0.015 = 0.065 = 6.5%

Percent Change in US GDP:

1929-30

-0.12235

1930-31

-0.16136

1931-32

-0.23298

1932-33

-0.04096

 

Review of Math: exponents, the mysterious e, and natural logarithms

 

You might not have used exponents recently so you may have forgotten the details.  To review, recall that exponents are simply a compact way of writing out multiplication (just as multiplication just means adding many times).  So 102 is 10 multiplied by itself twice, 10*10=100.  Then 103 = 1000, 33 = 27, and 25 = 32.  (Note that some computer programs, where superscripts are difficult, use the symbol ^ so they would write 10^3, 3^3, and 2^5.  Both these are often used when the exponent is a complicated function, so that the poor reader doesn't strain her eyes reading tiny superscript type.)

 

That is pretty simple, but then the mathematicians asked, what if these exponents are not nice counting numbers but zero, or negative, or fractions?  First, any number raised to a zero exponent is defined as being equal to 1.  Negative exponents are defined as raising the reciprocal to that power, so 10-2 is 1/100 = 0.01, 3-3 = 1/27, and 2-5 = 1/32.

 

Note that for numbers in decimal format, exponents mean moving the decimal point left or right: 3.1415*102 = 314.15; 3.1415*10-2 = 0.031415.

 

Fractional exponents are defined analogously to their whole-number relatives: if 102 is 10*10=100 then  "un-does" this, taking the square root so getting back 10.  Again, so this means that  and .

 

From these examples we can figure out some of the basic rules for what happens when two numbers, with a common base, are multiplied together or when a base-exponent pair is itself raised to a power.

 

First, what is 23 * 22 = ?  By the definition of exponents, 23 = 2*2*2 and 22 = 2*2 so 23 * 22 = (2*2*2)*(2*2) = 25.  This rule generalizes (not all examples do!) to the form that, given a base x, exponent A and exponent B,

.

This holds as long as x, A, and B are real numbers (positive, negative, fractions, zero, whatever).

 

Next, what if we had, instead,  =?  Again we just write out the simple meanings of those exponents.  Working from outside in, any number that is squared is simply multiplied by itself so .  The general rule, for a base, y, and exponents C and D, is that:

.

Again, this holds for all real numbers.  (I'm ignoring imaginary numbers only because economists don't often use those  contrary to many criticisms!)

 

You can see that the rules for exponents are, in some sense, taking the operations down a rank: multiplying two numbers with exponents means adding exponents; taking exponents of a number with exponents means multiplying the exponents.

 

Let me point out a couple of common applications of these rules (and a couple of others):

 

Next is logarithms.  These arise quite naturally if we want to un-do the operations of exponents.  From knowing that 103 = 1000, suppose we asked, 10 to what power equals 1000?  We could write 10x = 1000 or that log10(1000) = x.  The difference is only notational.

The Mysterious "e"

Mathematicians have come to depend on one particular special number when working with exponents, which is notated e.  It's like pi (π), 3.1415… because it's a number (called a transcendental) that goes on forever and seems quite mysterious until you've worked with it a while and gotten used to it.

 

For now, take this information on faith, don't worry too much about where this number comes from.  (If you want to prove that mathematics has logical holes, that might possibly all come crashing down, you're too late  Gödel did it decades ago!)  The number, e, is the area under a hyperbola (the equation y=1/x) rightwards from 1.  Where π is a basic measure for a circle (it is the area of a circle with radius of 1), e is a basic measure for calculus, because ex is a function of x with derivative ex.

 

The mysterious e can be understood in the context of finding interest rates.  Suppose you had $100 to invest at a 10% interest rate.  After a year, it would clearly be worth $110.  But suppose that another bank offered the same 10% rate, but with a bit of a difference: after six months they calculate the interest up to then (the 5%) and then again after six months they do the same.  So you get the effect of compounding: after one year, you'd have $110.25.  What if another bank offered to "compound" three times?  Four?  More?  In the limit, compounding daily or hourly or minutely, approaching "continuous compounding" which would get you a final balance of 100*e0.1 = 110.5171 (you could see this with a simple Excel sheet).

 

Now, in the real world, banks don't generally offer these continuously compounded rates, but it's nice for our theories.  It also comes in handy for growth and decay processes and solving differential equations.  The mathematicians have learned to love it, and even have figured out that eiπ (using i, the value of the square root of negative one, and pi) is 1, which brings together some of the strangest bits of math.

 

The inverse function, to un-do what ex does, is the natural logarithm, denoted ln(x).  This is the same as loge, log with base e.  The notation, ex=y, is asking, taking e to what power (y), will give me an answer of x.  The "natural" logarithm is natural because it uses the same number, e, that we figured out above as having desirable features for growth.  The main problem to watch for (particularly if you're making transformations of one variable to another) is that e cannot be raised to any power to make it equal to zero or less (negative).  So ln(0) or ln(-1) return nonsense answers (either NaN or some similar notation).

 

Outside finance, the macroeconomists probably make the greatest use of ex and ln(x), because of the connection with growth.  Suppose that an economy's GDP grows at 5% per year, every year, for 50 years (assuming continuous compounding, so that by the end of the 50 years, it's grown to nearly 12 times its original size.  A graph of raw GDP would look like this (starting at 1):

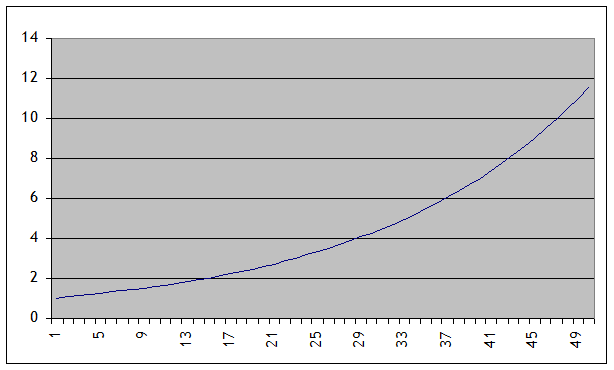
shooting up to ever-larger values, quickly becoming difficult to work with. (For instance, can you tell, just from the graph, how big the economy is after 25 years?  It's somewhere between 2 and 4 times as big as it started, but that's about all that you could tell.)  So taking the natural log of GDP would return a nice series like this:

It's transformed from a difficult graph to a simple line.  This is equivalent to plotting the previous graph on a log scale.

 

If the "log" referred to were to a base 10, then the graph would essentially be plotting how many zeros were in the GDP: from 1 to 10 is adding a zero, from 10 to 100 is adding another, etc.  When the "log" referred to is base e, then the interpretation as "zeros before the decimal" is no longer quite correct, but it's similar.

 

GDP values often have these growth paths, along with financial values (so the value of the Dow Jones average of the US stock market).

 

Politicians often play games with these sorts of numbers (knowingly or unknowingly) to confuse innumerate people.  Suppose an economy has been growing at 5% per year for many years, attaining last year's lucky GDP of 8888 per person.  In the last year, a new political party took power and now GDP per person is 9188.  The new political party might brag that they "grew" GDP by 300, and show a graph like this:

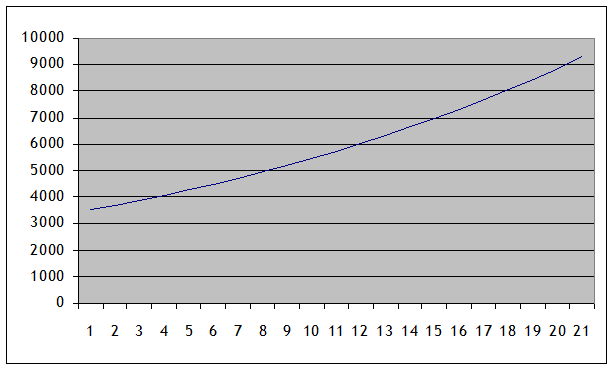
The slow-down in growth is tough to see.  But the growth rate did actually slow, which a log-chart would show, so that:

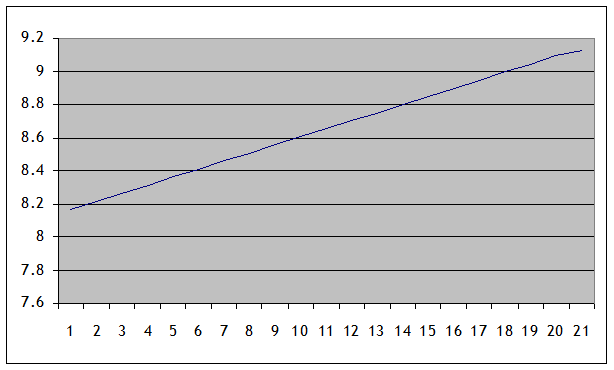
Where you can see that the line sags noticeably in the last year charted.  A 5% growth rate would have gotten the economy to 9332 not 9188, so the new policies could be criticized for stopping a twenty-year record of steady growth.

 

 

7. Crash lesson on derivatives ("double the coefficient rule")

 

The derivative gives us the slope of a function at a particular point. 

 

A line always has the same slope, so if the equation for a line is:

 

then the slope is  at every point.  (When X rises by 1, Y rises by m.)

 

But other lines have different slopes at different places.  Consider the function,

.  This is a parabola, a smooth curve that, near zero, has a very low slope, but then gets steeper and steeper.  Can we find a neat equation that tells us exactly how much steeper?  Yes: the derivative.  The derivative of  is  -- we take the coefficient on the x-squared term (which is 1) and double it.

 

If there were some other coefficient, say:

, then the derivative would be .

 

If there were both linear and squared terms added together, then we would proceed item-by-item:

 has derivative .

[Note: this only works for items added together.]

 

Want to know more?  Take calculus  it's fun and healthy!