Midterm Review K Foster, CCNY, Spring 2010

 

Some important concepts (not necessarily all!)

 

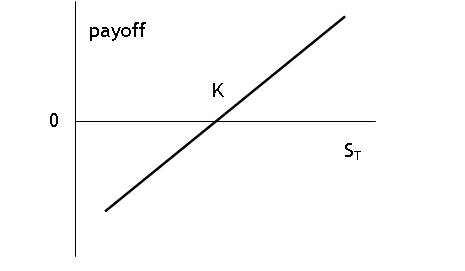
Payoff to Long forward position = S_T  K [Payoff to short position = - payoff to long position = K  S_T]

 

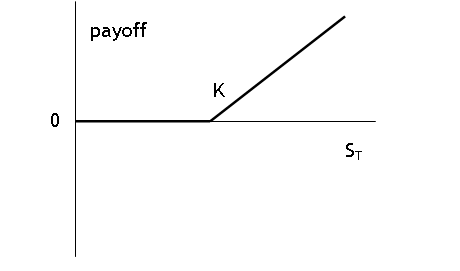
payoff to European call = max{0, S_T - K}

 

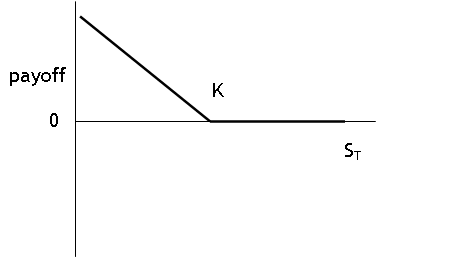
payoff to European put = max{0, K - S_T }

 

 

In continuous time ;in compounding at discrete intervals, m, then PDV(r,t,m) =  

 

Hedge is exchanging a volatile price (S_t becoming S_T) for a known price, F_t.

 

Basis Risk

 

Cross Hedging

 

change β of a portfolio

 

We might be confused because we might think that the forward price is a predictor of the price that will be set at that future date.  But it's not  the spot price is a predictor.

 

 F₀ = S₀e^rT. 

 

"cost of carry" is c so that for investment assets, ,

while for consumption assets, where y is the convenience yield, .

FX: .

f = (F₀  K)e^-rT. 

 

The intrinsic value of an option is its value if it were exercised today, either max(S_t  K, 0) for a call or max(K  S_t, 0) for a put.

 

C             value of American call option (sometimes distinguish between C₀ and C_T, the value now and value at maturity)

P             value of American put option

c              value of European call option

p             value of European put option

 

Six important factors affecting option prices:

1. Current stock price, S₀
2. Strike, K
3. Time to expiration/maturity, T
4. Volatility, σ
5. risk-free interest rate, r
6. dividends of stock over T

 

 

Upper Bounds for Option Prices

A call: c ≤ S₀ and C ≤ S₀; A put: p ≤ K and P ≤ K; in fact p ≤ Ke^-rT.

 

Lower Bounds for Option Prices

                c + Ke^-rT ≥ S₀ so c ≥ S₀  Ke^-rT

                p + S₀ ≥ Ke^-rT thus p ≥ Ke^-rT - S₀

 

Put-Call Parity

                c + Ke^-rT = p + S₀

or

c  p = S₀  Ke^-rT.

 

Bull Spread, Bear Spread, Box Spread, Butterfly Spread, Straddle, Strip, Strangle

 

Tree Model or Binomial Model

 

, , any contingent claim, G(Z), can be priced with the risk-neutral probabilities as  

Delta,