|
Homework 1 Possible Solutions
K Foster, Options & Futures, Eco 275, CCNY, Spring 2010 |
|
|
- Q 1.26.
To buy at $600 and sell at $800 locks in a profit of 200; this is a 200/600 = 33% return. So borrow as much as possible at 10% and invest at a guaranteed 33%!
- Q 1.27.
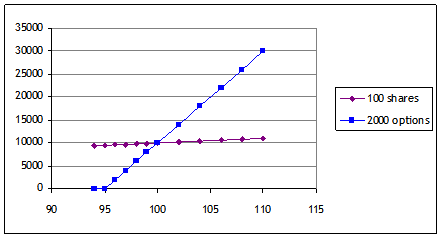
An investor with $9400 could buy 100 shares of stock at $94/share. Or could buy 2000 options (K=95); each option costs $4.70. If the stock goes to 95 then the investor makes $100 with the shares but loses with the options so her wealth is either 9500 or 0. Use Excel to make this chart, showing portfolio value for different values of the stock:
|
S = |
100 shares |
2000 options |
|
|
94 |
9400 |
0 |
|
|
95 |
9500 |
0 |
|
|
96 |
9600 |
2000 |
|
|
97 |
9700 |
4000 |
|
|
98 |
9800 |
6000 |
|
|
99 |
9900 |
8000 |
|
|
100 |
10000 |
10000 |
|
|
102 |
10200 |
14000 |
|
|
104 |
10400 |
18000 |
|
|
106 |
10600 |
22000 |
|
|
108 |
10800 |
26000 |
|
|
110 |
11000 |
30000 |
And the payoff graph clearly shows the difference: options could wreck the portfolio if the stock declines or doesn't gain much; they could really pay off huge if the stock does well.
- Q 2.27.
An investor has 5000 short futures at 4.50 with initial margin of 3000 and maintenance margin of 2000. If the price rises by 0.10 then the investor loses 0.10 on each contract so 500. So if the price rises to $4.70 then the investor will be down to her maintenance margin exactly and any future price rise will spur a margin call. If the price rises 3 more dimes (to $5.00) then the investor has lost 0.50 per contract or 1500.
- Q 2.28.
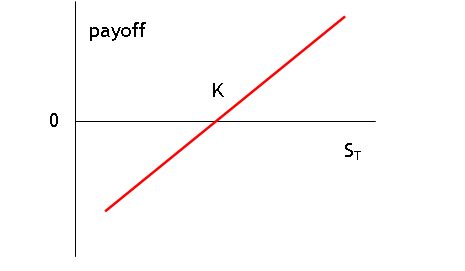
Find a position equivalent to long forward to buy at K and put to sell at K. Determine the payoff graph to this position: a long forward has a payoff graph like this:
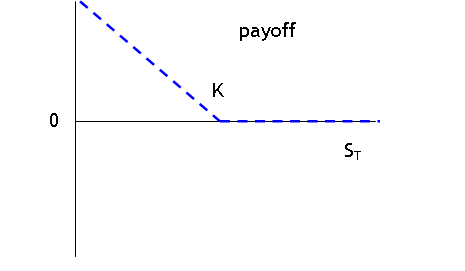
while the put pays as:
So the combined position pays as
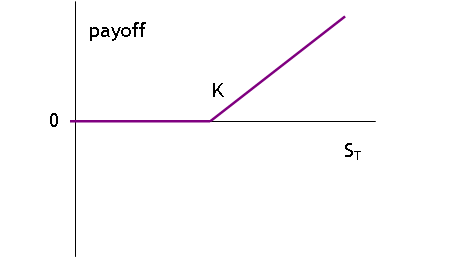
Where,
at a price greater than K, the net position is (S-K) bigger from the forward
and zero from the put so (S-K). When the
price is less than K, the position loses (K-S) from the forward but gains (K-S)
from the put so net zero. This should remind you of the payoff function
of a call. So we can replicate the
payoff to a call with a long forward and a put that will be important later.
- Leverage is at the heart of the popularity of options and futures. Consider if you have $10,000 equity to invest. You can put money into an investment that will return 10% in a year on the funds invested. What is your return on equity if you can't borrow? Now consider if you can borrow at 6% per year for up to half of the value of the investment. How much can you now invest? How much is left over, after you repay the loan? What is now your return on equity (ROE)? What if you can borrow up to 80% of the value of the investment? What if (this is the real estate case) you can put just 2% down and borrow the rest?
If
you invest $10,000 at 10% you will have $10,000 + 1000 = 11,000 at the end of
the year. This is a 10% ROE. If I can borrow at 6% then I can borrow
$10,000 and invest my own 10,000, so I will end up with 10% of $20,000 which is
2000. I must pay back the loan, which
costs 600, leaving me with 1400. So my
ROE is now 1400/10000 = 14%. If I can
borrow up to 80% then I would borrow $40,000 and invest $50,000 in total. This would return me 5000 and I would pay
back 2400, leaving me with 2600. This is
a 26% ROE! If I can borrow up to 98%
then I could invest $500,000, which would return $50,000. After paying back 6% of the 490,000 that I
borrowed (=29,400), I am still left with $20,600 a monstrous 206% ROE!
- Imagine that you had $5000 available to invest in futures contracts. Go online and carefully look at the requirements (for margin, fixed cost, etc) for entering into a contract. Describe a position that you would take (in any commodity, currency, index or bond that is traded standardly) using this imaginary $5000. Under what circumstances would you make a profit? How much? A loss? How much? (Each person in a study group should choose a different portfolio since next week we'll look to see who made the most money!)
Answers will vary.
- In the market for widgets, suppose that the current price is $30. You can enter into a forward contract to buy/sell widgets at $31.25 in one year and $31 in six months. The interest rate (at which you can borrow or save) is 4%. Assume that storage is costless. Consider an investment of $1m.
- If you bought widgets today and entered into a contract to sell them forward in a year, what would your portfolio be worth in 1 year?
Buying each widget at 30 and selling at 31.25 in a year nets me 1.25, which is 1.25/30 = 4.17% return on each dollar. So $1m becomes $1,041,667.
- If you bought widgets today and entered into a contract to sell them forward in six months, then at six months took the money and saved it (assume interest rates are unchanged), how much would your portfolio be worth in one year?
Buy widgets at 30, sell at 31 in 6 months, then invest at 4% so end up with 31*exp(rt) = 31*exp(.04*.5) = 31.62, which returns 1.62/30 = 5.42% return on each dollar. So $1m becomes $1,054,208.
- If, instead of saving the money for the second half of the year, you could buy/sell widgets at $31 and then sell after a year, how much would the portfolio be worth?
This is equivalent to the strategy in (a) so it returns 4.17%.
- If you put your $1m into the bank (saved it) how much would it be worth in a year?
Saving it would return 4.08% so 1,040,811.
- Now suppose that the margin is 50% what are the possible payoffs now?
At
a margin of 50%, borrow half, invest $2m, which returns 5.42% so netting (54,208*2) = $108,416. After paying off the 4% loan (paying 40,811),
$66,749 remains which is a 6.67% return.
- Now what if transactions cost $0.10 per widget what are the possible payoffs now?
With the previous strategies, $1m buys 33,333 widgets so the transactions cost is $3,333. Selling those same widgets then costs the same. So the net proceeds on (a) through (c) are reduced by $6,666; so (a) returns 35,000 so a 3.5% return; (b) returns $47,541 so a 4.75% return; (c) still returns 3.5%. The strategy in (d) has no transactions cost so it is still 4.08% return. The strategy in (e) costs 13,333 (since twice as many contracts) so the returns are $53,416 so 5.34% return.
So transactions costs change the net profit to buying widgets forward by enough to make it no longer profitable to invest in forwards, unless you could buy on margin.