Lecture Notes 1, Basics of Payoffs to Forward, Futures and Options K Foster, CCNY, Spring 2010

 

 

Learning Outcomes (from CFA exam)

Students will be able to:

§         define a derivative and differentiate between exchange-traded and over-the-counter derivatives;

§         define a forward commitment and a contingent claim;

§         differentiate the basic characteristics of forward contracts, futures contracts, options (calls and puts), and swaps;

§         discuss the purposes and criticisms of derivative markets;

§         explain arbitrage and the role it plays in determining prices and promoting market efficiency.

§         explain delivery/settlement and default risk for both long and short positions in a forward contract;

§         describe the procedures for settling a forward contract at expiration and discuss how termination alternatives prior to expiration can affect credit risk;

§         differentiate between a dealer and an end user of a forward contract;

§         describe the characteristics of futures contracts;

§         distinguish between futures contracts and forward contracts;

§         differentiate between margin in the securities markets and margin in the futures markets, and explain the role of initial margin, maintenance margin, variation margin, and settlement in futures trading;

§         describe price limits and the process of marking to market and compute and interpret the margin balance, given the previous day’s balance and the change in the futures price;

§         describe how a futures contract can be terminated at or prior to expiration;

§         explain why the futures price must converge to the spot price at expiration;

§         determine the value of a futures contract;

 

 

 

From Hull Chapters 1 & 2

 

Definitions

• Derivative: value depends on another variable

 

• Exchanges vs Over-the-Counter (OTC): OTC much bigger.

 

• Forward contract: agree to buy/sell a particular asset at given price and date/time.

 

• Spot contract: agree to buy/sell a particular asset at given price NOW.

 

S_t is the value of some asset at time t (so S₀ is value at time zero, the beginning; S_T is time at time T, often expiration date)

F_t is the value of some forward price at time t (the price at time t, of some asset to be delivered at date T>t; sometimes for clarity denoted F(t,T) the value at date t, of an asset to be delivered at T.

 

For now we just take these prices as given: some trader or exchange tells us what the price is.  (This is equivalent to saying that the financial markets are perfectly competitive so that our position will not affect the market price  we don't have market power.)  Later we will ask what the prices, theoretically, ought to be.  But first we have to understand the details of how portfolios can be constructed when the prices are just taken as given.

 

Long on forward: agree to buy at future date

Short on forward: agree to sell at future date

 

The particular price at which the option or forward trade will take place is Exercise Price or Strike Price (K).

 

The particular date by which the option or forward must be exercised is Expiration Date or Expiry or Maturity, T.

 

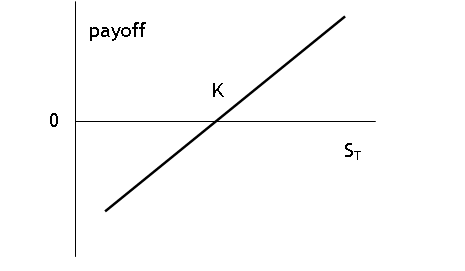
Payoff to Long forward position = S_T  K [Payoff to short position = - payoff to long position = K  S_T]

 

Forward vs Future contracts: futures are traded on an exchange in regulated sizes

 

Call Option: the right (but not the obligation) to BUY a particular asset by a particular date at a particular price

 

Put Option: the right (but not the obligation) to SELL a particular asset by a particular date at a particular price

 

The asset, from which the option value is derived, is the underlying asset or underlier.

 

American vs European options: American options can be exercised at any date up to the expiry; European options can only be exercised on the date. 

 

Puts and calls can be bought when they are "in-the-money," "out-of-the-money," or "at-the-money" (ATM).  In the money means that the option would have value today given the current trading price; out of the money means it would have zero value if the expiration date were to be right now; at the money means that the strike price is just equal to the current price of the underlying asset.  (so, for a call, S_t>K is in the money, S_t=K is at the money, S_t<K is out of the money; for a put S_t<K is in the money, S_t>K is out of the money, S_t=K is at the money).

 

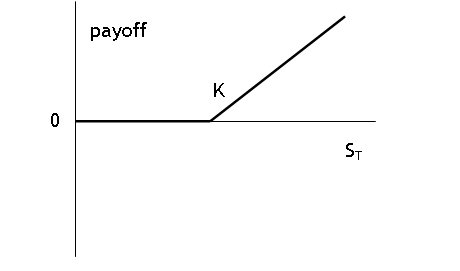
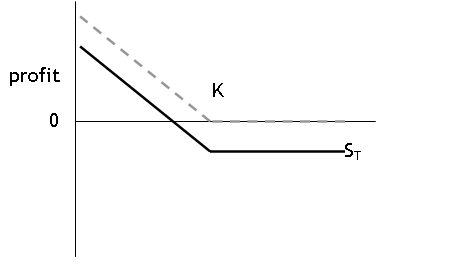
payoff to European call = max{0, S_T - K}

 

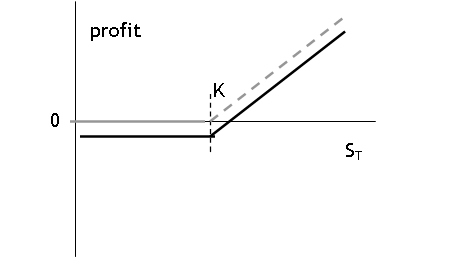
Note "profit" is different since call has a cost:

 

payoff to European put = max{0, K - S_T }

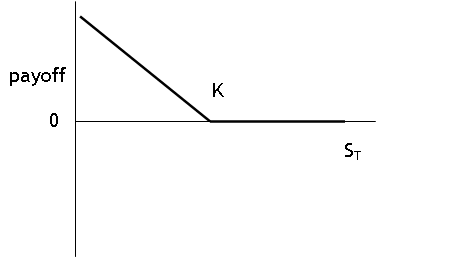
Note that payoff to put is bounded.

 

Again profit is different since put also has a cost,

 

Types of traders:

• hedgers – re
  
  uce risk of other positions
• speculators
  
   bet on market movements (but speculation is in the eye of the beholder!)
• arbitrageurs
  
   make multiple positions and profit from the gaps, make riskless or nearly-riskless profits (some risk is, for example, counterparty risk)

 

These derivatives markets are popular largely because of the enormous leverage available; although leverage is not necessarily bad  one trader's leverage is another trader's cheap insurance.

 

The essential transaction: pay a little bit of money now, have a possibility of getting a lot of money later.  If these are insurance premiums and coverage payouts, then a big ratio of payout to premium is cheap insurance.  If these are initial margin and profit, then a big ratio of profit to margin is speculation.

 

Examples of each type of trade (where margin allows leverage)

• If I own a stock, then buying a ATM put allows me to lock in the sales price: for each $1 that the stock goes below its current value, the put pays off $1 so the positions offset exactly.  I still get upside (although I pay for the insurance so it is less).
• If I must deliver a stock at a future date then buying a call allows me to lock in the price that I'll pay, again with some upside (to me) risk
  
   if the price falls below the strike then the stock can be purchased even cheaper.
• In both cases I pay for the insurance.  If the price is, say, 10 cents per dollar of stock value, then a speculator can, with just 10 cents of capital, put a large bet on the direction a stock will move.  If a speculator sells a ATM put then she will make a 10-cent return (100%!) if the asset rises in price (since the put would not be exercised).  If the asset falls in price by just 10 cents then the position is bust and the speculator will get a margin call.  Opposite for selling a call
  
   will make 100% return if price falls, but lose money really fast if the price rises.
• forward

 

 

Chapter 2

Chapter 2 has much detail about the intricacies of futures markets.  Read it closely.  The most relevant to this class are below.

 

Supply & Demand for forward purchases

• markets are highly liquid and very deep
• commoditized (perfect substitutes)
• very sophisticated participants
• so assume highly elastic supply & demand curves; nearly horizontal

 

Positions usually Closed Out not delivered so buy an offsetting position and book the monetary gain or loss

As delivery date nears, futures price should converge to spot price: as  then  

Occasionally (in oil market about a year ago) these prices diverge

Both parties need to understand all of the details of delivery

Futures contracts have daily settlement (so cash flows) to ensure that both parties stay whole in case of a problem (such as the Financial Crisis)