Lecture Notes 10

Lecture Notes 10,The Greeks

K Foster, CCNY, Spring 2010

Learning Outcomes (from CFA exam)

Students will be able to:

§ explain how an option price, as represented by the Black–Scholes–Merton model, is affected by each of the input values (the option Greeks);

§ explain the delta of an option and demonstrate how it is used in dynamic hedging;

§ explain the gamma effect on an option’s price and delta and how gamma can affect a delta hedge;

From Hull Chapter 17

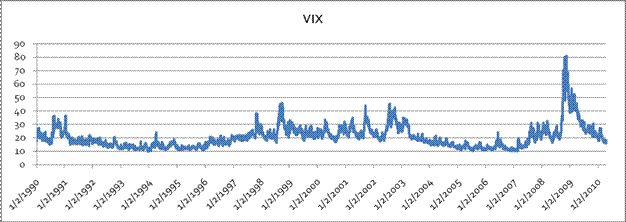
When finance people talk about "The Greeks" they don't mean the lunchcounter on Amsterdam Ave. "The Greeks" in this context refer to the changes in the price of an option when some of the parameters are changed.

So what?

Consider a call option which is far, far in the money. There was some news item that launched the stock way, way up. When the stock price gets very high above the exercise price (assuming the volatility isn't too high), the call price approaches its intrinsic value. Another way of putting it, the change in the call price, , is approximately the same as the change in the stock price that underlies the option, . Or we could write that, for very high S, the ratio, , is approaching one. This ratio, , is called V. We used V back in Chapter 11 to construct trees (and warned you that V would be back, like a cheesy horror movie villain who keeps rising from the dead to attack again!).

Is Delta always equal to 1? No, that wouldn't be very interesting! Delta shows the relative weights of an option versus one share of the underlier, that would have to be held, in order to make two portfolios give the same return (or in order to make a single portfolio riskless). Most institutional investors are in the market because they're looking to change (or at least shift around) the risks of their current portfolio. Delta is one of the first tools to understand how the price of some security and its derivative change together.

Getting Naked and Covering Your Assets

Consider the position of a financial institution (say, an investment bank) that has just written a big option. Their customer bought it, in hopes of getting a lot of money. The bank is worried that their customer might get a lot of money out of them! Assume that the option is an ATM call, for stock with S₀ = 100 = K, r=0.02, T=1, s=0.25, so the Bl-S-M price is 10.87. If the bank sold 100,000 of these options then they just got $1,087,000. But if the stock rises in price, they could be out even more. If the stock is 110 by the end of the year, the bank will be out $1m and will barely break even. If it goes up by more, they're losing money. Their upside risk is limited: if the price of the stock goes down then they don't pay out more, but they don't get more than the initial amount of the sale (about $1m). If they just decide to take on the risk, that’s a "naked" position. A "covered" position buys the stock that needs to be delivered, but while that covers the bank if the stock price goes up, it exposes the bank to the risk of the stock going down.

A stop-loss policy might seem to combine the best of both of these strategies. When the stock price is below exercise, the call is out of the money and a naked position is most advantageous. When a stock price is above exercise then the call is in the money and a covered position is best. Can close monitoring of the position allow a bank to hedge the risk? Well, it can do a little bit, but the problem is that this takes an enormous number of trades particularly if the stock price bumps up and down, over and under the exercise.

Delta Hedging

As we developed in Chapter 11, if a $1 move in the stock value produces a $V move in the option value, then we can construct a riskless portfolio by holding V shares per option. This portfolio is "delta neutral" because it has a zero net delta. So is hedging that easy? Not quite. Consider this table of Bl-S option prices, for different stock prices:

The slope of the line (which is V) is always changing. Delta is about equal to 0.5 when the stock price is about 100 (which is K) but as it falls then the delta also falls (the line gets less steep). Oppositely, as the stock price rises then delta rises as well, but the call price rises towards its intrinsic value – it can never be worth more than that, so the delta can never be greater than one. In the example at the beginning, of employee stock options, we went through that.

So a delta-hedged portfolio would have to be re-hedged as the stock price changed: at first, when S0 is 100, delta is 0.58. If the stock price drops to 95 then delta is 0.5 so the portfolio would need to be rebalanced. A portfolio which is rebalanced often is a "dynamic-hedging scheme"; if it is just set and not changed, it is a "static-hedging scheme".

Forward and future positions can also contribute to the delta of a portfolio: forwards have a delta of 1 since as the current price rises/falls the forward price should also rise/fall in step; future positions have a delta of e^rt.

How does delta change with the stock price? If we look at the slope of the line above we could sketch the change, or use the Bl-S formulas to calculate:

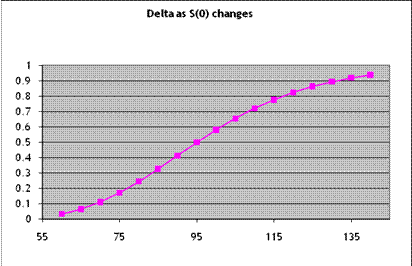
This is the delta for different values of the stock price. (This is the approximate value, for short intervals.) If we differentiate the Black-Scholes formula we find that for a call and, for a put, .

Up to this we've been discussing the delta of a single option price, but we can extend the idea to a portfolio of assets (on any variety of instruments) that has a value of P. The delta of the whole portfolio is then

and we can either evaluate this value by simulation or as the weighted average of the deltas of each asset in the portfolio (where the weight, w_i, is how many dollars are invested), so that:

If we go back to the graph of how an option price varies with changes in the underlying stock price,

we can see that the curvature of the graph determines how good or bad a static hedge can be. If the delta is already up near 1, then small changes in the stock price won't change delta by much and so the hedge will still be pretty good. Or similarly if the delta is down near zero already. But in the middle, where the price of the option is quite sensitive to the stock price, a dynamic hedge would require frequent rebalancing. So we want to know how much delta changes when the stock changes – this is another one of the Greeks, Gamma (G). Gamma measures the curvature of how the option price changes with the stock price underlying.

Gamma is the rate at which delta changes, as the stock price changes. Since delta is itself the rate at which the option price changes as the stock price changes, that means that gamma is the second derivative of the option price, with respect to the underlying stock price, so for some call option price, c:

For a call or put, twice differentiating the Black-Scholes formula gives

At-the-money options with short maturities have very high gamma.

Another of the Greeks is Theta (Q), the time decay. Theta tells how the portfolio value changes over time – it is the predictable component of how the values of each part of the portfolio will change.

For options, a decrease in the time to expiration will shrink the value of the option towards its intrinsic value (zero if out of the money or the payoff if it is in the money).

If we differentiate the Black-Scholes formulas, we find that:

, which will be negative.

For a put, the differentiation gets:

which is usually negative.

Theta is not something to be hedged against – it is known and entirely predictable, however it is useful because it can give us estimates of Gamma. For a portfolio of assets, the change in the delta of a delta-neutral portfolio depends on theta and gamma,

Portfolio managers commonly want to hedge against Gamma, but a problem arises: Gamma is the curvature of the rate of portfolio value change and is not sensitive to linear changes. A share of the underlying stock has zero gamma so gamma-neutrality requires an asset with a non-linear payoff.

If a delta-neutral portfolio has gamma of G₀, and some option has gamma of G₁, then it would take G₀/G₁ options to gamma-hedge (although this would generally change the delta, so it would take some more fiddling to get the right mix. A portfolio that is both delta-neutral and gamma-neutral is hedged against small movements in the stock and is also hedged against sudden large movements that would hinder the ability to dynamically rehedge.

These Greeks can be combined if we recall the basic Black-Scholes-Merton differential equation (derived from the heat equation) that (for a single option price, p, or for a portfolio, P):

so now that we have defined , , and , we can re-write it as:

which relates these Greeks together. Also of course, if V=0 then a delta-neutral portfolio will have so that theta and gamma have similar magnitudes and opposite signs.

For completeness' sake, we can define Rho, , as the change in the portfolio position when the risk-free interest rate changes, . However this is not commonly used.

The final of "the Greeks" is Vega, , the change in Volatility. The Black-Scholes-Merton equation assumes that volatility is constant, so this parameter is a bit of an oddball. That might explain why, as the Greek scholars reading this may have already noted, there is actually no such Greek letter as "vega". (It's a star.) But it's too late now, the terminology is embedded.

So we define = , the amount that the portfolio value changes when volatility changes.

For an option, the Black-Scholes formula gives = .

The underlying asset is not sensitive to the volatility; but option prices are sensitive to volatility. Making a portfolio be delta-neutral, gamma-neutral, and vega-neutral is a difficult balance and requires not only positions in the underlying security but also at least two different options.