|
Lecture Notes 12,Credit Risk, Credit Derivatives, and CDO & CDS Securities K Foster, CCNY, Spring 2010 |
|
|
Learning Outcomes
Students will be able to:
· explain the basics of credit risk and popular strategies for hedging and mitigating
· know about the basic Credit Derivative securities as well as the risks involved
· list some "exotic" options in addition to the vanilla options already studies
Other Greeks
From Wikipedia, some Greeks that I'd never even heard of (bordering on silly):
http://en.wikipedia.org/wiki/Greeks_(finance)
|
With respect to: |
||||
|
Change in: |
Spot Price S |
Volatility |
Expiry (τ) |
Rate (r) |
|
Value (V) |
Δ Delta |
ν Vega |
Θ Theta |
ρ Rho |
|
Delta (Δ) |
Γ Gamma |
Vanna |
Charm |
|
|
Vega (ν) |
Vanna |
Vomma |
DvegaDtime |
|
|
Gamma (Γ) |
Speed |
Zomma |
Color |
|
|
Vomma |
Ultima |
|||
Hull Ch 22, Credit Risk
As the financial crisis has shown, one of the most important (but difficult to quantify) risks is Credit Risk: the risk that some company will go bankrupt and be unable to satisfy its liabilities.
Credit ratings, provided by agencies like S&P, Moody's, or Fitch (as well as other smaller companies) are supposed to provide indications of credit risk, tiering bonds into general categories. Historically default rates have been higher for lower-rated bonds.
However as recent news has spotlighted, these credit rating agencies are not always good at predicting defaults. Their ratings of individual companies are based on publicly-available information, which have been extensively analyzed and compared with past publicly-available data. However some companies are risky in ways that the rating agencies are not able to perceive, for instance fraud. And certain sectors have sudden transitions into behavior that is not at all like the past; for example mortgage-backed securities (more on this later). Although the rating agencies were spectacularly wrong with some products, they continue to provide useful analysis of many other securities.
A bond holder is primarily interested in: 1. the probability of default, and 2. the recovery rate. If the bond does not default then the bondholder gets 100% of the promised value of the bond. If the bond defaults then the bondholder gets less; how much less is a complicated question. The recovery rate is the infamous "haircut" where bondholders get less than 100% of the money that they were contractually supposed to get. Sometimes this haircut comes quick, sometimes it comes after a long bankruptcy court proceeding.
For simple cases a bond with, for example, a 5% chance of defaulting and a 40% recovery rate, should pay about 5%*40% = .05*.4 = .02 = 2% over the risk-free rate.
Companies regularly engage in asset swaps, where they agree to "swap" a bond's cashflow for a different rate, often LIBOR plus some basis points. These transactions can be seen as providing some information about market perceptions of credit risk in those bonds.
But actual historical default rates and recovery rates do not imply spreads of corporate bond yields that are as high as those in the market. For example, the bond above might trade at 4% over risk-free even though the historical data imply 5% default and 40% recovery so just 2%. Why this gap?
The reason from theory is that the bonds are priced using risk-neutral probabilities not actual real-world probabilities. But this is equivalent to saying that bonds are priced by the market as having some extra margin of risk, which is generic to the markets. Bonds do not default in the simplistic way mentioned above; they tend to default most in a recession or a financial crisis when many default together. Corporate bonds are less liquid so difficult to transfer into cash. So the spread of corporate yields over risk-free is historically higher than would be implied by a simple model.
To look at historical levels, I went to the Federal Reserve's website which has a nice "Data Download" interface, and got historical Treasury (1, 5, and 10-year), Aaa, & Baa interest rates. These are:
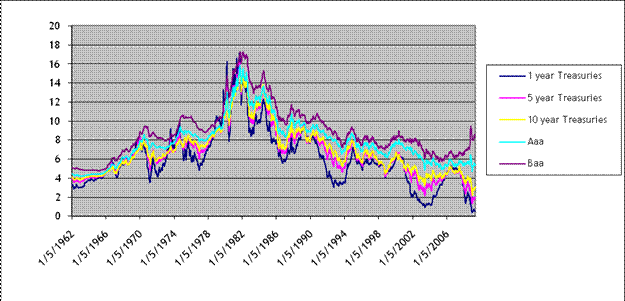
Which shows how the market interest rates generally move together, although a look at just the spreads (the difference of Aaa minus Treasury 5-year, etc) shows the extent to which this tracking can break down in times of financial stress.
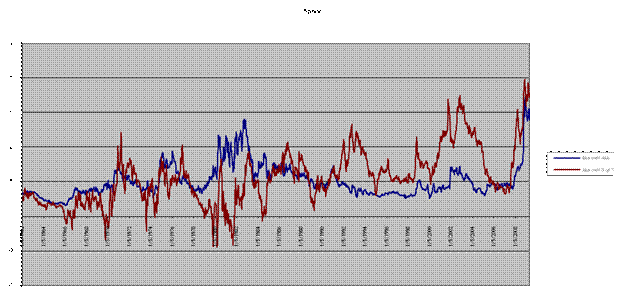
Modeling any individual bond is difficult enough; modeling the structures of interrelations of many bonds is quite difficult to achieve in a parsimonious but realistic manner.
However the individual versus systemic implications can be different! For example, it may be optimal for me to include a clause that, if my counterparty is downgraded, they will need to put up more collateral. However if every one of the other institution's counterparties all put in that exact same provision, then a downgrade can precipitate immediate bankruptcy. (Which then means that the ratings agencies have enormous power!) Or we can get a scenario such as how Goldman pushed AIG away from solvency with more cash calls.
Hull Chapter 23, Credit Derivatives
Read this one closely, it's fun! The first sentence gives a clue, "The most exciting developments in derivatives markets since the late 1990s have been in the credit derivatives area." (Hull, p 525)
Credit derivatives are what killed AIG and precipitated the most serious financial crisis since 1929 – exciting is an understatement!
If you like close reading, you can follow along as Hull
revised this chapter from the 6th to the 7th edition
(with a few notes hinting at trouble, since in summer 2007 the credit markets
had lost traction) and, surely soon to come, the 8th edition –
probably a substantial re-write!
This chapter is a must-read for anyone who wants to consider themselves financially literate. It gives excellent definitions and a birds-eye view of the CDS and asset-backed securities (CDO) markets and how SPVs began.
A CDS is a Credit Default Swap, is a fancy name for a simple insurance deal: I pay a regular rate (basis points calculated on the bond notional) but if the bond defaults then I get paid the entire principal. Just like if I had insurance on my house: I'd pay regular premium and then, if fire destroyed my house, I'd get a big payment from the insurance company.
The CDS spread is the rate paid for insurance, the premium.
The exact definitions of "what is default" can be awfully tricky and complicated.
The Financial Crisis showed that there is a "spiral" problem in the CDS market as well, where a few companies sell this insurance (so are exposed to large losses in the event of a bad shock) while their counterparties think they're hedged because they've bought insurance against the risk of default by their first counterparty.
There are indexes of CDS spreads such as CDX NA IG (for
North American companies) and iTraxx
Forwards and options on CDSs were naturally extended.
CDSs were wrapped with fixed/floating swaps to make Total Return Swaps, which are often used as a financing tool, like a repo, that minimize credit risk between the parties.
Asset-Backed Securities are synthetic securities created from baskets of other securities. These could be as simple as a market portfolio (e.g. the SPY tracks the S&P 500) that is created from a bunch of stocks. Or it can be backed up by any number of thinly-traded (or never-traded) assets such as mortgages, loans, credit card debt, etc. (In a stretch, Lloyds of London could be thought of as a financial engineering company.) These synthetic securities state a payout structure which is (supposed to be) more credit-worthy, with senior tranches, mezzanine tranches, and equity tranches (the lowest of the low, re-branded).
Collateralized Debt Obligations (CDOs) are synthetic securities of bonds or other securities.
These were ideally supposed to work like insurance products, providing safety due simply to the Law of Large Numbers.
If a bank has, say, 1000 mortgages, each worth $200,000, then these are worth in total $200m. If each mortgage has an individual and idiosyncratic risk of defaulting, and the probability of default is, say, 5% and there is a 50% recovery rate, then the bank would expect that, each year, 50 mortgages would default and the portfolio would lose $5m or 2.5% of its value. The mortgages would be priced to reflect this default risk. For now suppose that the mortgages paid 7% in total, so generating a cash flow of $14m (gross or $9m net) for a 4.5% return. (There is a separate risk of early repayment but we'll ignore that for now.)
But the bank could re-arrange these 1000 mortgages into a separate entity (usually SPV) that would collect all of the mortgage payments and send out the cash to investors according to different schedules. The simplest example would be to slice it into 2 securities: one would take on most of the risk while the other would be much less risky. There is likely to be a $9m net cash flow after defaults. If the low-risk half (senior tranche) could get $4.5m first while the high-risk half (equity tranche) got ($14m - $4.5m – defaults), then all of the risk is shifted to one set of securities. If defaults are lower then the risky security gets more return and vice versa. The low-risk side only takes a hit if defaults are more than $9.5 in total (they're expected to be just $5m).
Of course the low-risk side could get less than a 4.5% return (fees paid to bank!) because of this security, just like any basic insurance product where people are willing to pay more than the expected value of the loss.
Slicing the cashflows into more than 2 parts is straightforward.
Exotics
from Hull Chapter 24
Bermuda options (between European and American) – allow early exercise but only on particular dates. Or early exercise only during part of option life. Or strike price might change.
Forward Start options or Compound Options (a call on a call or a put on a call or ...)
Chooser Options: after some time period, holder chooses whether it will be call or put.
Barrier Options: knock-in or knock-out if asset price hits a pre-specified level. "Down & Out" call is regular call that is "knocked out" if call goes far out of the money. Then "Up & Out," "Down & In," and "Up & In."
Binary Options: discontinuous payoff, e.g. "cash or nothing call" pays either nothing or a fixed amount Q (not proportional to payoff of ordinary call).
Lookback Options: depend on min or max of asset value in some reference period.
Shout Options: holder "shouts" to writer at some point before option expires, then holder gets greater of option expiration value or asset value at time of "shout."
Asian Options: payoff depends on average asset price during life of option – either the asset price or strike price is averaged.
Exchange Options: payoff will exchange assets.
Rainbow Options: choose delivery from several assets (e.g. bond futures).
Basket Options: payoff depends on a basket of multiple assets.
Volatility Swap: swap actual volatility for some fixed volatility.