Lecture Notes 6, Simple Stock Models, moving toward Tree Models (Ch 11)

K Foster, CCNY, Spring 2010

 

 

Learning Outcomes (from CFA exam)

Students will be able to:

§         calculate and interpret prices of interest rate options and options on assets using one- and two-period binomial models;

 

 

Begin a very simple model

 

Use Matlab (or even Excel) to create models of stock price movements.  What model?  How complicated is "enough"?

 

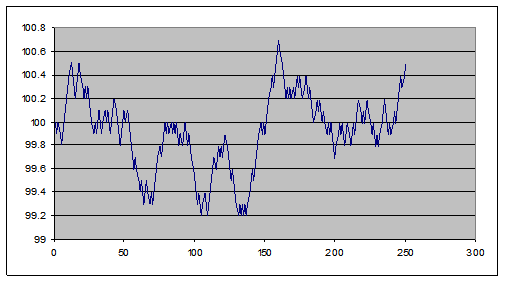
Start really simple: Suppose the price were 100 today, and then each day thereafter it rises/falls by 10 basis points.  What is the distribution of possible stock prices, after a year (250 trading days)?

 

Excel

 

First, set the initial price at 100; enter 100 into cell B2 (leaves room for labels).  Put the trading day number into column A, from 1 to 250 (shortcut).  In B1 put the label, "S".

 

Then label column C as "up" and in C2 type the following formula,

=IF(RAND()>0.5,1,0)

The "RAND()" part just picks a random number between 0 and 1 (uniformly distributed).  If this is bigger than one-half then we call it "up"; if it's smaller then we call it "down".  So that is the "=IF(statement, value-if-true, value-if-false)" portion.  So it will return a 1 if the random number is bigger than one-half and zero if not.

 

Then label column D as "down" and in D2 just type

=1-C2

Which simply makes it zero if "up" is 1 and 1 if "up" is 0.

 

Then, in B3, put in the following formula,

=B2*(1+0.001*(C2-D2))

 

Copy and paste these into the remaining cells down to 250.

 

Of course this isn't very realistic but it's a start.

 

Then plot the result (highlight columns A&B, then "Insert\Chart\XY (Scatter)"); here's one of mine:

 

Matlab

First,

S0 = 100; % initial price

TT = 250; % number of trading days

 

Then,

stockprice = zeros(1,TT);

stockprice(1) = S0;

 

And we model the "up or down by a ten bps" with the "unifrnd(0,1)" command, which selects a random number between zero and one.  If it's greater than 0.5 then we assume the price goes up; if less than 0.5 then the price falls.

 

So this evolution of the price would be:

is_up = unifrnd(0,1) > 0.5; % one if up; zero if down

is_down = ~is_up; % is zero everywhere is_up is one and vice versa

 

Of course this isn't very realistic, but it's a start.

 

So have the computer walk through a year's time like this:

for indx = 2:TT % 250 trading days

    is_up = unifrnd(0,1) > 0.5; % one if up; zero if down

    is_down = ~is_up; %

    stockprice(indx) = stockprice(indx-1)*(1 + 0.001*(is_up - is_down));

end

 

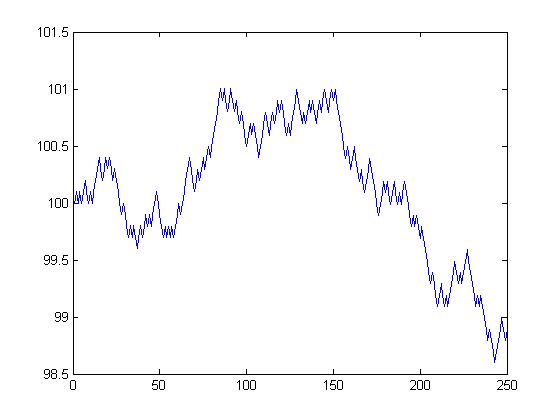
Then see what it looks like:

plot(stockprice)

This is one of mine:

 

(this is program mod_stock_l6a.m)

 

Simple, right?

 

That's only one run; we might want to see more to get an idea of all of the possible outcomes.

 

 

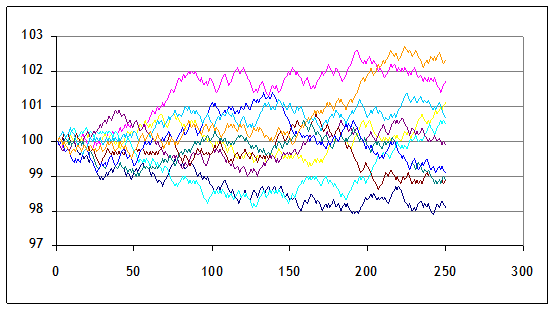
Here are 10 series (copied and pasted the whole S, "up," and "down" 10 times),

 

 

To do this in Matlab, we first create a big matrix to hold all of the stock price paths:

possib_pr = zeros(TT,20); % 20 possible paths

And then put another loop around the first one that we wrote (remembering to save the results of the price evolution into the big matrix).

 

for out_indx = 1:20

    stockprice = zeros(1,TT);

    stockprice(1) = S0;

    for indx = 2:TT % 250 trading days

        is_up = unifrnd(0,1) > 0.5; % one if up; zero if down

        is_down = ~is_up; % is zero everywhere is_up is one and vice versa

        stockprice(indx) = stockprice(indx-1) * (1 + 0.001*(is_up - is_down));

    end

    possib_pr(:,out_indx) = stockprice'; % puts the 250 days into a column of 'possible price paths'

end

 

Then, again, plot the output.

plot(possib_pr)

 

 

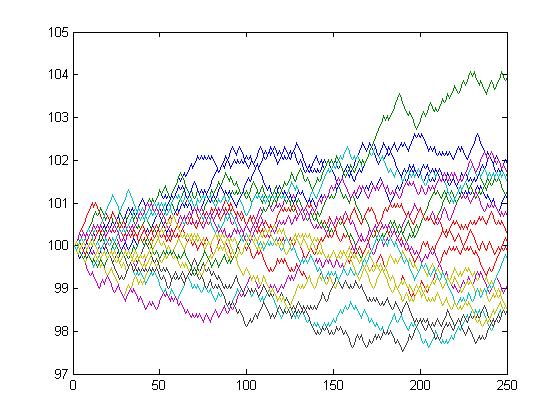
We're not done yet; we can make it better.  But the real point for now is to see the basic principle of the thing: we can simulate stock price paths as random trips.

 

The changes each day are still too regular  each day is 10 bps up or down; never constant, never bigger or smaller.  That's not a great model for the middle parts.  But the regularity within each individual series does not necessarily mean that the final prices (at step 250) are all that unrealistic.

 

I ran 2000 simulations; this is a histogram of the final price of the stock:

 

 

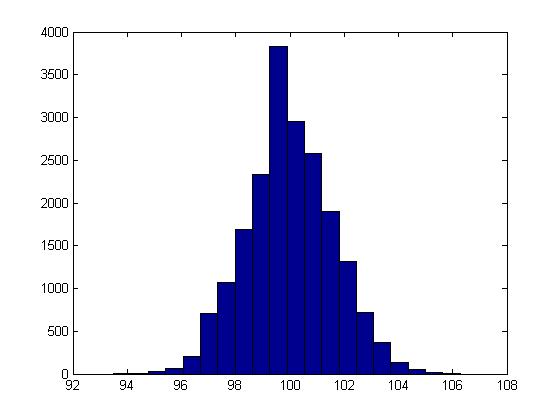
It shouldn't be a surprise that it looks rather normal (it is the result of a series of Bernoulli trials  that's what the Law of Large Numbers says should happen!).

 

With computing power being so cheap (those 2000 simulations of 250 steps each took far under a minute even on my slow laptop) these sorts of models are very popular (in their more sophisticated versions).

 

It might seem more "realistic" if we thought of each of the 250 tics as being a portion of a day.  ("Realistic" is a relative term; there's a joke that economists, like artists, tend to fall in love with their models.)

 

There are times (e.g. Hull's Chapter 11) when this very simple model can be useful, because the fixed-size jump allows us to keep track of all of the possible evolutions of the price.

 

 

Tree Models

 

 

From Hull Chapter 11

 

One way of solving problems of option valuation is to split the problem into tiny steps: first, suppose that the stock would either rise or fall by some discrete amount.  Of course this is a terrible assumption if we're talking about a period of time like 3 months, but it's not a bad assumption is we're talking about a period of time like a second.  And if we can solve it, then we can model the first second, then the next and the next, up to three months!  (Or, we might not have that many steps, but at least we can have enough to get a decent approximation.) The full model is called a tree, because each branch splits into more branches and so on.

 

But first we have to solve the 2-step tree.  Suppose the stock is worth 100.  Either it goes up to 110 or down to 90 after a time interval.  This tree would be drawn like this:

 

 

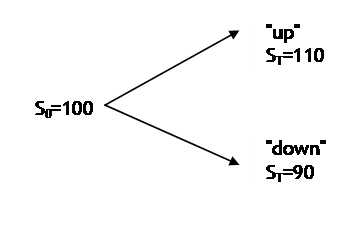
The upper node has a value of 110 and the lower node has value of 90.  There is some probability of going up or down (in our first simple model we set this probability to  but it could take any value from zero to 1); it is adequate to specify just one probability in this simple case since pdown = 1  pup. 

 

There is also a riskless asset, a bond, that can be purchased at price of 1 today and will payoff (1+R) after a year  this is just a formalization of the idea that agents can borrow and lend at LIBOR.

 

Binomial Model

explanation from Tomas Björk book

 

Two assets, Bt and St

2 times, 0 & 1

B0 = 1, B1 = 1 + R

S0 = s,

, with probability pu and pd;

alternately

, where  

 

A portfolio is (x,y), x units of Bond and y units of Stock,

 

Assume x, y can be any real number; no transactions cost or bid/ask spread

 

Value of a portfolio is Vt = xBt + ySt

so V0 = x + ys, V1 = x(1+R) + ysZ

 

Arbitrage portfolio would have V0 = 0 but V1>0

 

Arbitrage free means d ≤ (1 + R) ≤ u

Implies that (1+R) is a linear combination of d & u;

i.e. there are some α, β such at

(1+R) = αd + βu, α+β=1, α>=0, β>=0

or, alternately,

(1+R) = qd d + qu u, qd + qu = 1, qu>=0, qd>=0, if we interpret as 'probabilities' under EQ

this is "risk-neutral probability" or "martingale" probability

 

 

can calculate these risk-neutral probabilities with a bit of algebra,

 

 

Then any contingent claim, G(Z), can be priced with the risk-neutral probabilities as

 

To show this, want to find some portfolio that has the same value as G(Z) at time 1; so

 

which means finding x and y such that

(1 + R)x + suy = G(u)

(1 + R)x + sdy = G(d)

These solutions are:

 

 

 

So option values are calculated as if in a risk-neutral world  but of course this is not an actual description of the world, nor need it be.  Also hold for all investors whether risk-neutral or otherwise.

 

Example: Stock is worth 100 now; it goes up to 110 (so u=1.1) with probability 70% (pu = 0.7) or goes down to 90 (d=0.9) with probability 30% (pd = 0.3).  A call has strike of 105 so it is worth either 5 or 0.  Assume R=0 to make things really simple.  So from the definition of qu and qd, we have (1+R) = qd d + qu u, qd + qu = 1; the first equation becomes 1 = 1.1qu + .9qd, so qd=qu=0.5.  From this we find that the price, G0, of the call with value of 5 or 0, is EQ[G1] = qu*5 + qd*0 = 2.5.  This seems odd since the option has a 70% chance of expiring in the money  shouldn't it be worth at least $3.50?!  But the $2.50 price comes from the risk-neutral rate not the actual probabilities.  Why is this?  Because the portfolio (paying off $5 if "u" and $0 if "d") can be replicated by holding (x,y) units of (bonds, stocks).  How many?  Plug into the formula above or solve: if "u" then x(1+R) + ysu = G(u), or x+110y = 5.  If "d" then x(1+R) + ysd = G(d) or x + 90y = 0, so subtract the second equation from the first and get y= 5/20 = .  Then x = -22.50.  A portfolio that is short 22.5 bonds and long  of a stock has initial price of x+ys = -22.5 + (100) = 2.50.  If the stock goes up then the portfolio has value -22.5 + (110) = 5; if the stock goes down then the portfolio has value -22.5 + (90) = 0.  So this portfolio replicates the option payout.  If some sucker were to offer to buy options at $3.50 (thinking that, since he has a 70% chance of making $5, that seems like a good bet) then I could create as many options as I want (at a cost of $2.50 each) and sell them for $3.50.  (Create the option with the opposite holding of the replicating portfolio: long 22.5 bond units and short  of a stock would pay out 22.5  (110) = 5 if "up" and pay out 22.5  (90) if "down".) 

 

Now do for R=0.02  will the option be more or less expensive?

 

Alternate Derivation, using Hull's notation

We return to the previous model, with a stock worth 100 currently, which either goes up to 110 or down to 90 after 6 months.

 

Suppose I have a short position in a call with strike of 100 (ATM) and I want enough stock to make the total portfolio riskless between the two nodes.  How much stock does it take?  Call it "".  If the stock rises to 110 then I would have 110* worth of shares minus 10 for the short call, for total 110 - 10.  If the stock went down to 90 then I would have a portfolio worth 90.  What delta would give the same payoff in each state?  Set 110 - 10 = 90 so =10/20 = 0.5.  So a portfolio with a half share of stock and one short call would always have the same payoff (either 55  10 if the stock goes to the up node or 45 if the stock goes to the down node) so its value must grow at the risk-free rate interest rate  or else there would be arbitrage opportunities, if there were 2 portfolios with the same (riskless) payoff but different values. 

 

Here we'll slip into continuous-time interest, so the present value of this payoff in 6 months had better be 45e-rT = 45e-0.5r.  If the current risk-free six-month zero rate is 4.5% then this is 45e-0.045*0.5 = 45e-0.0225 = 45* 0.97775 = 43.9988.  So the current value of this portfolio .5*S0  c = .5*100  c = 50  c must equal 43.9988 so c = 6.001.

 

Generalize this to a stock that moves either up by some amount "u" or down by "d" (so u > 1 and d < 1).  So the value of a portfolio, with  shares of the stock, is either uS0 or dS0.  Also assume that we have a short position in one option that has value of fu or fd, if the stock goes up or down.  So the portfolio value in the "up" node is uS0 - fu; the portfolio in the "down" case is dS0 - fd.  We can find a value of  that makes the portfolio riskless; i.e. find  such that uS0 - fu = dS0 - fd or  (  from the previous notation).

 

Denote f as the current value of the option, so we must have that S0 - f = e-rT(uS0  fu) and f = S0(1  ue-rT) + e-RTfu.  Some more algebra (plus the equation for  ) gives us that

                .

 

(Compare with above, in the discrete-compounding example, where we have (1+R) instead of eR but no other real difference in the formulas.)

                                                                                              

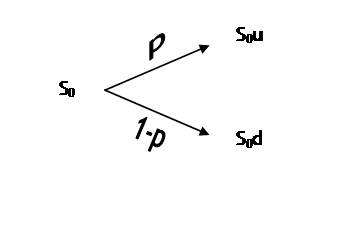
In a risk-neutral world, the p and (1  p) terms can be interpreted as the probabilities of an up or down movement, so that the tree can be sketched as:

.

 

Although, again these "p" are risk-neutral probabilities NOT real probabilities in the world.

 

Now suppose that the six months were divided into two steps: U or D and then another u or d again (so we could have any of the sequences Uu, Ud, Du, or Dd).  Typically we would allow the tree to be "recombining" so that Ud and Du get us to the same place:

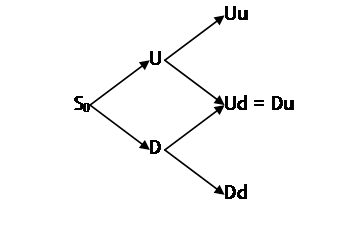, which is equivalent to setting each up or down movement to the same factor: U=u at each step and D=d at each step.  So a stock that initially went up from S0 would be worth US0; if it then fell it would be US0d.  If it went first down then up, it would be DS0u; if u=U and d=D then these are evidently the exact same numbers!

 

We take the time interval at each step to be , where m is the number of steps in the tree.  Then solve the tree backwards (from right to left)  the final nodes are the simple two-step trees that we just solved; do the whole last column of two-step trees, then back up and use the answers just found to solve the next-to-last column.

 

Puts work the same way as calls.  Trees are often used to value American options or other more exotic options (that are path-dependent) since at each node the computer can check whether early exercise is optimal.

 

For trees with more than a very few outcomes, this calculation becomes boring and is best suited for a computer.  Back in the old days, a thirty-step tree might have been considered to be pretty awesome; as computing power keeps increasing the number of possible steps can be increased as well (with diminishing returns, of course).

 

How do we create "good" tree models?  As we go on, we will discuss the volatility of the stock, σ.  Generally we set  and .

 

While we're talking about , let's mention "delta".  Financial practitioners sometimes talk about "doing the Greeks" or other such expressions.  Delta, , is the first important concept: how many shares of stock must be held, per option held, to create a riskless hedge.  (Sometimes called delta hedging.)  In general delta will change over time.  A company that wants to keep a hedged portfolio must balance the costs of rebalancing with the benefits of keeping a close hedge.

 

Numerical Examples

First show that the probability case gives the same answers for the call option as does the risk-free no-arbitrage argument.  The stock has a p chance (in the risk-neutral world) of moving up to 110 and a (1  p) chance of going down to 90 so its expected value is 110p + 90(1  p) which must be equal to 100erT.  (Note  there is no negative sign there!)  The p that solves this equation is   -- again, note that this probability is determined entirely by the risk-free rate and the up/down values, NOT the actual probability of occurrence.  The call has a payoff of 10 in "up" and zero in down so its expected payoff (under the risk-neutral probability) is 10p = 6.13.  The present value of this is 6.13e-rT = 6.001.  This is precisely the answer recorded above.

 

We can work the trees with other options (puts, American options, various other derivatives).  For example, return to the one-step tree, with S0 = 100, uS0 = 110, and dS0 = 90.  What if we had a put option at the money?  It would have a zero payoff in "up" and a payoff of 10 in "down".  So the portfolio that is short the put and has  of the stock would return 110 in "up" and 90 - 10 in "down".  Set these equal and find  = -0.5.  Yes, it's negative: that means the portfolio should be short a half share of stock.  The riskless portfolio returns -55 at the end of the period so its present value is -55e-rT.  The portfolio is currently worth -0.5S0  p = -55e-rT so that p = 55e-rT - .5S0.  With T=0.5 and r=0.045 (just like the first example) this is 53.776  50 = 3.776.

 

(Recall the put-call parity formula, c  p = S0  Ke-rT, does that check out? Yes: 6.0012  3.776 = 100  100e-rT = 100  97.775 = 2.225.)

 

If the put had a different strike price, say of 97.50, then we would still follow the same procedure.  This put would payoff 7.50 in "down" so the portfolio that is short the put and with  of the stock would return 110 or 90 - 7.5 so  = 7.5/20 = - 0.375.  This riskless portfolio would have present value of -41.25e-rT, which we would set equal to the current market value of -0.375S0  p = -37.5  p.  Solve to find p = 2.832.

 

Now let's try a 2-step model.  Still keep S0 = 100.  Now let the percent change be 5% so first the stock either rises to 105 or falls to 95; then it moves to 110.25, 99.75, or 90.25 (as shown in the table below).  We won't worry that the center node is no longer precisely 100 since that's not important for this exercise.

 

 

110.25

 

105

 

100

 

99.75

 

95

 

 

 

90.25

Now T = 0.25 because it takes two steps to get to a half of a year; still keep r = 0.045.  Consider a call option with strike price of 100.  Its value at each node is now shown below the stock price:

 

 

110.25

 

 

10.25

 

105

 

 

?

 

100

 

99.75

?

 

0

 

95

 

 

0

 

 

 

90.25

 

 

0

Since two of the last three nodes are zero, the option price, when the stock price is 95, is zero.  We only need to calculate the top branch of the tree.  So figure what  gives 110.25 - 10.25 = 99.75, which gives  = 0.976.  So the portfolio is 105 - c = 99.75e-rT = (0.976)99.75e-0.045*0.25 = 96.286.  So c = 6.214.  Put this into the tree:

 

 

110.25

 

 

10.25

 

105

 

 

6.214

 

100

 

99.75

?

 

0

 

95

 

 

0

 

 

 

90.25

 

 

0

Now we need only solve the one-step tree, with stock price and option values:

 

105

 

6.214

100

 

?

 

 

95

 

0

Now, with a different delta, we set 105 - 6.214 = 95;  = 0.6214.  This riskless portfolio, .6214*100  c, must have value of e-rT(95) = 58.376.  So c = 3.768.  The complete tree is:

 

 

110.25

 

 

10.25

 

105

 

 

6.21433

 

100

 

99.75

3.767599

 

0

 

95

 

 

0

 

 

 

90.25

 

 

0

 

 

Finally, if you know your statistics you'll recall that repeated binomial statistical draws converge in probability to a normal distribution (Laplace is usually cited as being the first to solve this).  That's where we're headed next.

 

Tree Examples

 

 

  1. Stock is currently 10, goes up to 11 or down to 9 after 1 year, rate is 3%.  What is value of call with K=10.50?  Put with K=9.50?

So u=1.1 and d=0.9, exp(1*0.03)= 1.03045.  Solve 1.03045 = qdd + quu, qd + qu = 1 to get 1.03045 = qdd + (1- qd)u, 1.03045 = 0.9qd + 1.1(1 - qd), 1.1  1.03045 = .2q to find qd = 0.3477, so qu = .6523.  Alternately could solve, as in Hull, S0exp(1.03) = qdS0d + quS0u, which just multiplies by S0.  These Q values give risk-neutral probabilities so call is worth 0.5 if up, 0 if down so currently PV(.6523*0.5) = PV(0.3261)=.3165; put is worth 0.5 in down, 0 if up, so PV(0.3477*0.5) = PV(.1739) =.1687. 

Or delta-hedging method has some amount of stock, , such that value of 11 - 0.5 = 9.  So =0.25 (thus 11=2.75 and 9=2.25).  So PV of this riskless portfolio must be exp(-.03)*2.25 = 2.1835.  So 10 - c = 2.1835 and c=.3165.

If both had the same strike we could check Put-Call Parity, if c-p = S-Ke-rt (it does check out).

 

  1. Stock was at 200/$.  It was considered that, in 1 month, it could have gone to 190 or 210.  So u= 1.05 and d=.95.  If the interest rate (was 4%, what were ATM calls and puts valued?

Again start with exp(rT), now equal to 1.0033.  Set this equal to qd + (1-q)u so 1.0033 = .95q + 1.05(1-q) and 1.05  1.0033 = .1q so q=.4666 and (1-q) is .5334.  So EQ(call) = 10*.5334 = 5.3339; PV(EQ(call))=5.3161.  EQ(put) = 10*.4666 = 4.6661; PV(EQ(put)) = 4.6506.

 

Or by -hedging so 210 - 10 = 190; =.5 so portfolio is worth PV(95) = 94.6839, which is currently equal to 200 - c, so c=5.3161 again.

 

  1. Next if zoom went to 180, now considered that in a month could be 170 or 190, and interest rate is 2%, what are ATM calls & puts?

Now exp(rT) = 1.0017.  Set this equal to qd + (1-q)u so 1.0017 = .9444q + 1.0556(1-q) and q=.4850, (1-q) = .5150.  So ATM call is worth PV(EQ(10)) = exp(-(1/12).02) * .5150 * 10 = 5.1415; ATM put is 4.8418.