Lecture Notes 7, Wiener Processes and Itô's Lemma

K Foster, CCNY, Spring 2010

 

 

Learning Outcomes (not directly from CFA exam for this one)

Students will be able to:

§         see how we use Itô's Lemma and the underlying stochastic calculus to set up the Black-Scholes-Merton option pricing result;

 

Basic Calculus

Recall from basic calculus the definition of the derivative: examine the limit,

                 

and if both the left-hand-side (lhs) and right-hand-side (rhs) limits are equal, then we call this limit the derivative,

                .

 

Re-write this to show that, for very small values of h,

                , or, in a switch of notation, replacing h with Δx,

                .

This we can interpret along the lines of the Taylor Theorem, that for small values of x, the term xf'(x) is a good approximation to f.

 

The Taylor Theorem says that for a differentiable function, we can approximate local changes with derivative(s),

                 

Which relates to the interpretation of the derivative above as basically stating that (since of course 1! = 1) the first two terms are a 'pretty good' approximation to the value of the function at f.  We can usually think of the x2 and x3 and higher-order terms as going fast towards zero, so fast that they are of negligible importance.

 

Recall/Learn from Advanced Calc

If we have a function of two variables, say a production function that output is made by two inputs, capital and labor, then we would write this as

                 

and then define the marginal productivity of each input separately, as the amount by which output would increase if one input were increased but the other input held constant.  This is notated mathematically as .  If we had some general polynomial function to represent output, say that  (a funny-looking production function, I know, but the math works out easy).  Then  and . 

 

The total differential, dy, is defined as equal to the sum of the partials,

.

This has an easy economic interpretation: if L goes up by a little bit, ΔL, how much does output change? By MPL*ΔL.  If K goes up by ΔK, then output rises by MPK*ΔK.  If both L and K change by small amounts then we get the total differential above.

 

Now since we are suppressing the functional notation, we could write the total differential, more cumbersomely but equivalently, as .  This is useful because, to find the second derivative, we need to find how the partial derivative with respect to L changes as K changes (i.e. how the marginal productivity of labor is affected by having more capital) as well as vice versa (how the marginal productivity of capital changes with having more labor  i.e. how the partial derivative with respect to K changes with L.  So it is natural to consider the second partial derivative just like a regular second derivative.

 

To put this into a bit more generality, given G(x,y) then .

 

What if, now, we have a chain of functions, so the function, G( ), is a function of time, t, and another function, X(t)?  In finance it is natural to think of G( ) as a payoff function of a derivative that depends on the time (whether it is at expiration) and the stock price (itself a function of time).  But for now just allow G(t,X(t)) a general existence.  Then we can express the change in the value of the function as

 

where since X is itself a function of time we can write

, or, in full functional notation,

,

which makes clearer that we first take the partial with respect to the first argument, then take the partial with respect to the second argument (which is itself a function so we use the Chain Rule).

 

So we've got some fearsome-looking math notation but we haven't done anything more sophisticated than using the Chain Rule.

 

Next we review some basic statistics that you learned.

 

Basic Stats

Recall the definition of the sample variance, that

                 

which estimates the true population variance, which is

                 

And note that if the mean is zero, µ=0, then the variance is equal to the expected value of the squared random variable;

.

 

In statistics it is often convenient to use a normal distribution, the bell-shaped distribution that arises in many circumstances.  It is useful because the (properly scaled) mean of independent random draws of many other statistical distributions will tend toward a normal distribution  this is the Central Limit Theorem. 

 

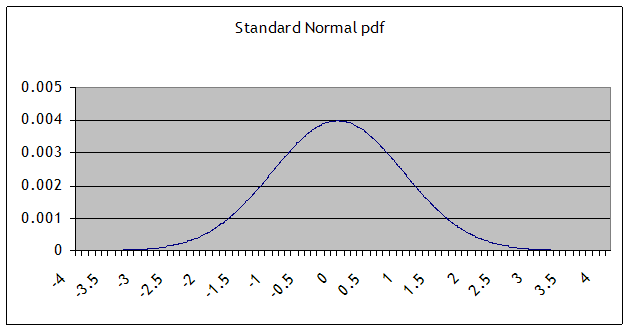
Some basic facts and notation: a normal distribution with mean µ and standard deviation σ is denoted N(µ,σ).  (The variance is the square of the standard deviation, σ2.)  The Standard Normal distribution is when µ=0 and σ=1; its probability density function (pdf) is denoted pdfN(x); the cumulative density function (CDF) is cdfN(x) or sometimes Nor(x).  This is a graph of the pdf (the height at any point):

and this is the CDF:

 

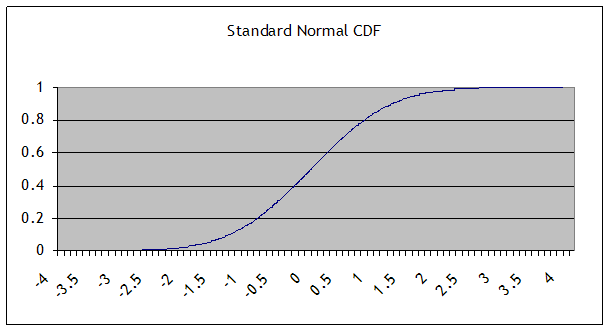
One of the basic properties of the normal distribution is that, if X is distributed normally with mean µ and standard deviation σ, then Y = A + bX is also distributed normally, with mean (A + µ) and standard deviation bσ.  We will use this particularly when we "standardize" a sample: by subtracting its mean and dividing by its standard deviation, the result should be distributed with mean zero and standard deviation 1. 

 

Oppositely, if we are creating random variables with a standard deviation, we can take random numbers with a N(0,1) distribution, multiply by the desired standard deviation, and add the desired mean, to get normal random numbers with any mean or standard deviation.  In Excel, you can create normally distributed random numbers by using the RAND() function to generate uniform random numbers on [0,1], then NORMSINV(RAND()) will produce standard-normal-distributed random draws.

 

In Matlab, of course, we can use x = random('Normal', 0, 1);

 

Now for the Main Act

I'm going to do some (more) rather sloppy math here, in the interests of communicating the concept rather than all of the details.  We'll go through Hull's derivations later, but it may be most helpful to first get the idea.

 

In simple modeling of stock prices we had a return in two parts: a general drift and an error.  We can represent the return on a security as , where the term, aΔt, is the drift and bW is an error term.  Focus on the error, W.

 

For a first approximation we might use the normal distribution to model this error.  We want it to have a zero mean or else there would be arbitrage opportunities.  Then we want to think of how our uncertainty about a stock value changes with the time horizon; it seems reasonable that as a future date gets farther off, our uncertainty would increase.  The range of variation that I expect a stock to be in, after one year, is much larger than the range I'd expect after just a day.

 

This is equivalent to assuming that ΔW is normally distributed with mean zero and variance equal to the distance between time increments, so .  The W notation is used since these are called Wiener processes: it is continuous everywhere but no-where differentiable.  It is commonly used in many physical sciences.

 

Hull explains that this is a plausible model of a stock return: if we model the stock price at some date as being normally distributed, what is the distribution of the price when we're halfway to that date?  One of the advantages of the normal distribution is that the distribution at some nearer date can also be normal.  The mean is an easy linear function.  But what about the variance?  Halfway to the final date, the expected distribution of prices should be less volatile.  We'll assume that the variance is proportional to the time interval, so when we're halfway to some date, the variance of the normal distribution is half of what it will be at the end.  This makes sense because we observe that, over a longer interval, price changes tend to get larger: the daily changes of the stock market are much smaller than the yearly changes. 

 

Side Note: The basic property, that the distribution is normal whatever the time interval, is what makes the normal distribution {and related functions, called Lévy distributions} special.  Most distributions would not have this property so daily changes could have different distributions than weekly, monthly, quarterly, yearly, or whatever!

 

We can keep doing this on and on, finding that the variance at a point half-way there is half of the original variance  like Zeno's famous paradox of Achilles and the tortoise.

 

With some mathematical hocus-pocus we can prove that this converges to a Wiener process.  This could look something like this:

 

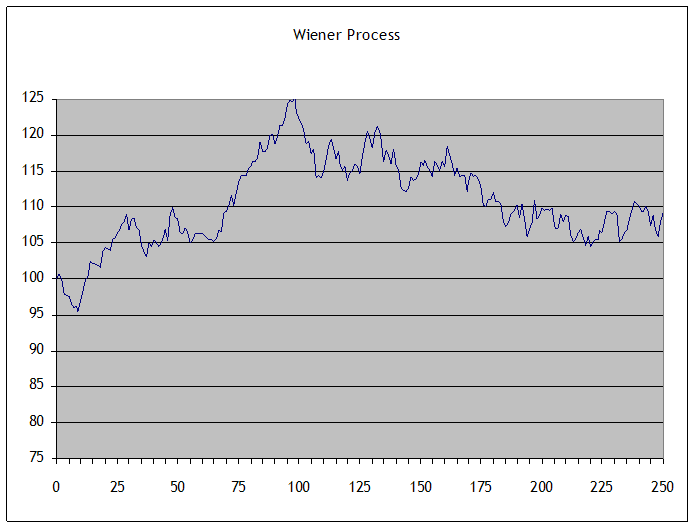
Recall from calculus the idea that some functions are not differentiable in places  they take a turn that is so sharp that, if we were to approximate the slope of the function coming at it from right or left, we would get very different answers.  The function, , is an example: at zero the left-hand derivative is -1; the right-hand derivative is 1.  It is not differentiable at zero  it turns so sharply that it cannot be well approximated by local values.  But it is continuous  it can be continuous even if it is not differentiable.

 

Now suppose I had a function that was everywhere continuous but nowhere differentiable  at every point it turns so sharply as to be unpredictable given past values.  Various such functions have been derived by mathematicians, who call it a Wiener process (it generates Brownian motion).  (When Einstein visited CCNY in 1905 he discussed his paper using Brownian motion to explain the movements of tiny particles in water, that are randomly bumped around by water molecules.)  This function has many interesting properties  including an important link with the Normal distribution.  The Normal distribution gives just the right degree of variation to allow continuity  other distributions would not be continuous or would have infinite variance.

 

Note also that a Wiener process has geometric form that is independent of scale or orientation  a Wiener process showing each day in the year cannot be distinguished from a Wiener process showing each minute in another time frame.  As we noted above, price changes for any time interval are normal, whether the interval is minutely, daily, yearly, or whatever.  These are fractals, curious beasts described by mathematicians such as Mandelbrot, because normal variables added together are still normal.  (You can read Mandelbrot's 1963 paper in the Journal of Business, which you can download from JStor  he argues that Wiener processes are unrealistic for modeling financial returns and proposes further generalizations.)

 

These Wiener processes have some odd properties.  Return to the notion of approximating a smooth process by a Taylor series, where we want to know the properties of some function of a Wiener process.  So given the definition of , we want to find .  Then the Taylor formula would be

                 

or,

                 

where we can approximate G as its first derivative, times the size of the step, x.  And the existence of the derivative means that, in a sense, the second order and higher terms are very small  small enough that the first derivative is the limit as the size of the step goes to zero.

 

As we noted, Wiener processes are not differentiable.  This is largely because of the second-order term: the random variation is "too big".  But we can try to figure out a way to take account of the second-order term.

 

We argued intuitively that the variance of the Wiener process is , that the variation is proportional to the time step.  In our recollection of basic statistics we said that the variance of any mean-zero random variable is ; this implies that .  Looking at the equation above, showing the Taylor approximation, this shows that the second-order term does not die off  it is of magnitude t.  Since  this means that the second-order Wiener process term is of the same order as the first-order drift term.

 

Being a bit more careful, we can start from  and then just idly find .  Again the variance of W is of a higher order, , that the variance of the Wiener process is given as the size of the time-step.  So .  The middle tern does, however, drop out since Δt and ΔW are each very small, and multiplying two very small things (which are uncorrelated) by each other will give an even smaller result.  The ΔW2 term doesn't drop the same way because ΔW is correlated with itself (its variance).

 

So returning to the Taylor approximation,

                ,

or, switching from Laplace's notation to Liebnitz'

                .

Now substitute our basic definition of , as well as our deduction above that , so

                .

This is a genuinely weird result.  Stop a moment and consider it: the variance, b, of the underlying process, suddenly emerges to have a direct influence on the level of G (since it multiplies by Δt).

 

This is the beginning of the larger result, known as Itô's Lemma. 

 

We might wish to analyze a more general function, say .  This is a good representation of the payoff to a derivative, since it depends on t (time to expiration) as well as the value of the underlying security, x(t).  We'll move to a continuous time representation of x and write  (with "d" instead of Δ).

 

In this case the first order partial derivatives are .  We can omit the second order terms from the first arguments since these are of order .  But the second order terms from the second argument is  where, as we previously found,  so the second-order term is .  So the total derivative of G, dG, is

                 

and then we substitute in the term  to get

                .

 

And that ugly bit of mathematics is Itô's Lemma.  It shows a general formula for how the first order effect (the expected value) is affected by the second-order terms  not just the variance but also the second "derivative" of the function of the Wiener process.

 

To take the most ordinary instance, take , so the x are price changes and G(x) gives the value of the stock.  Then  and ; of course .  Substitute these into Itô's Lemma to find

                 

Since this beast that we're calling  is the stock price, , we can re-write the equation as

                ,

which shows that the mean of the stock price return is determined in part by the variance.

 

Hull's Explanation

One of the other basic properties of Wiener processes is that they have a Markov property (or representation).  This means that their history is irrelevant: the current value gives the best forecast.  This coincides with our model of weak stock market efficiency, the theory that current prices embody all possible information.  If there were useful information to be derived from the stock's history, then someone else would have likely already found it and used it.

 

Formally, z is a Wiener process if:

 

So if we define N = T/t, then zT =z0 + .

 

A generalized Wiener process adds a drift rate that is a known function and a variance function, so now x is a generalized Wiener process, dependent on z, a standard Wiener process, if dx = a dt + b dz, where a and b are constants..

 

An Itô process is a further generalization, where now a and b are given functions of x and t, so ; for short discrete changes we assume that a and b are constant over some range so that approximately , where you will note that we've inserted the identity that .

 

We often model a stock's percentage return as a generalized Wiener or Itô process, dS = µSdt + σSdz, or dS/S = µdt + σdz; in discrete time this is S/S = µt + σε .

 

Itô's Lemma

 

If we have a function, G(x), where x is an Itô process, , then Itô's Lemma just tells us that finding G(x) is more complicated:

.

 

This requires a good bit of calculus to get your arms around.  If you recall the math, good.  If not, just remember the formula and keep this around so that after you take some more math classes you can come back to Mr. Itô and his Lemma.

 

Recall from calculus how to find a Taylor expansion, for some function G(x), which is near G(x0) so we want to find G = G(x)  G(x0):

; that G is differentiable means that the higher-order terms (x2 and up) are tiny so we have a good approximation.

 

Next, if G were a function of both x and y, G(x,y), then the total derivative is:

 

Normally, a function that is differentiable has the higher-order powers (x2 and y2 and xy) again die off at a high rate so we would be left with just the terms involving x and y.

 

Now if this function, G(x), has an x that is an Itô process, , or, if we drop some of the extra notation, that ; in discrete time this is .

 

Itô's Lemma tells us that finding G(x) is more complicated, that

.  It might be easier to remember if we break it into the relevant parts: if we did not have a stochastic component, then if we differentiated G(x(t,z),t) then we'd have ; then Itô's Lemma just adds in a term, .

 

How can we show this?  Taylor's theorem gives us that:

 

 

Normally we could drop the second-order terms because we're letting the dx and dt terms get infinitesimally small so that (x)2 and (t)2 get even tinier.  But in this case,  so .  How is the last term different from the first two?  It does not have t to any higher power (squared or to the 1.5 power).  So it doesn't drop out  we have to incorporate it into the Taylor expansion.  We can write  and substitute it into the Taylor series, so

.

 

From here we just simplify.  If  then its variance is one so the expected value of ε2 =1 and that term drops out.  Also we substitute in  and so

, or, rearranging,

 

 

 

That is the result that you were promised at the beginning of this section.  Congratulations if you made it this far!