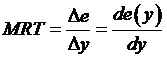Lecture Notes 3

Economics of the Environment and Natural Resources/Economics of Sustainability

K Foster, CCNY, Spring 2011

Short Review of Production

Production Externalities

In the simplest case, we can examine a firm making a single private (rival and excludable) output and incidentally a single public (nonrival and nonexcludable) output (for now, we assume that this public good is disliked). An easy example could be a power plant which makes electricity and pollution. (Actually a variety of sorts of pollution, which affect different groups of people: carbon, mercury, NOX, and sulphur dioxide are the main ones.)

In this case the production can be shown as being like a production possibility frontier but with the pollution increasing along with the output, something like:

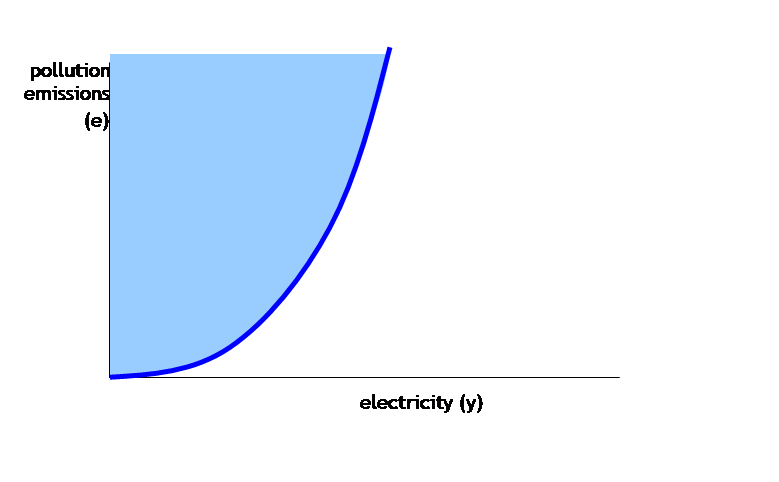
The firm can choose any combination of electicity & pollution within the light blue area. Clearly, however, the firm would be foolish to choose a point inside the area; the points at the dark blue line are efficient. These are the production possibility frontier. They are efficient because there is no way to increase the output of electricity without also increasing the output of pollution (this would not be true for points in the interior).

At any point along the frontier of production possibilities, we can define the marginal rate of transformation as the change in output of pollution per change in output of electricity – the slope of the line. With the notation of e for pollution emissions and y for the output of the firm, the marginal rate of transformation, MRT, here is , where is the function linking the amount of emissions generated as determined by the amount of output produced. We can think of electricity generation as transforming some amount of a public good (in this case clean, unpolluted air) into a private good (electricity).

This interpretation of the choice along the production possibility frontier as representing a choice of marginal rate of transformation allows us to compare firms and make statements about the relative efficiency.

Suppose there are two firms which, for some reason or another, have different emissions per unit of output. Graphically this would be represented as:

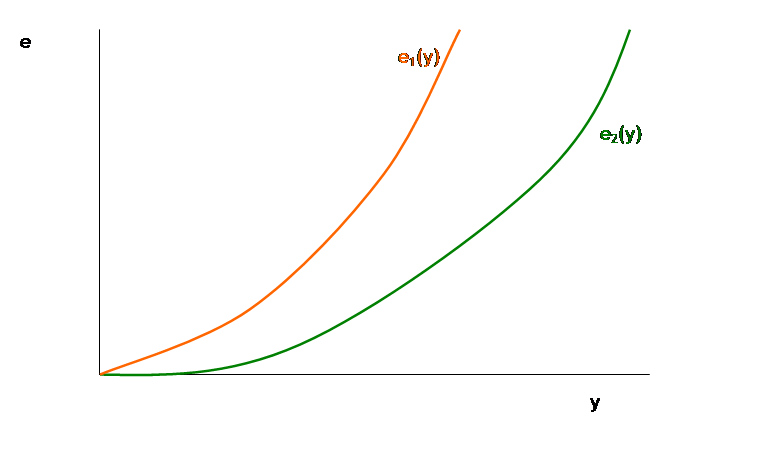
If they each produced the same amount of emissions, they would of course be able to generate different output levels, but their marginal rates of transformation would also be different.

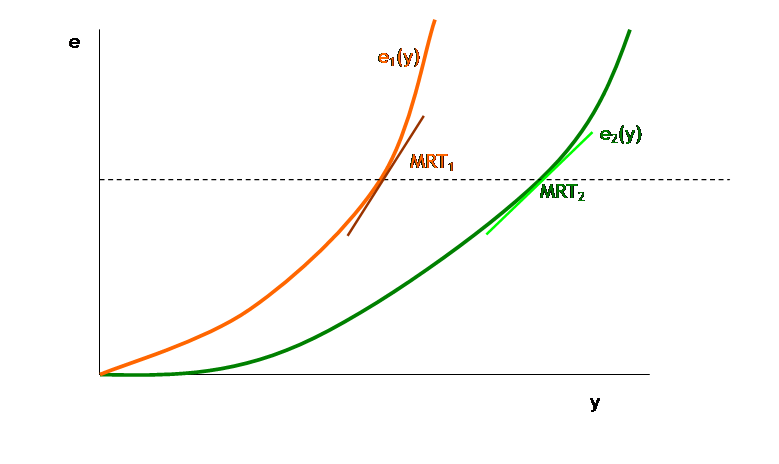
Clearly the marginal rate of transformation of firm 2 is lower than the marginal rate of transformation of firm 1. This means that when firm 2 generates one more unit of output, it creates fewer emissions than firm 1 does. This means that, if firm 2 were to make one more unit of output while firm 1 made one unit less – keeping the total output of the two firms at the same level, the increase in emissions from the second firm would be (in absolute value) less than the decrease in emissions from the first firm. So total emissions would be smaller even though the output was kept constant.

Consider a simple numerical example, where but . This is plotted as:

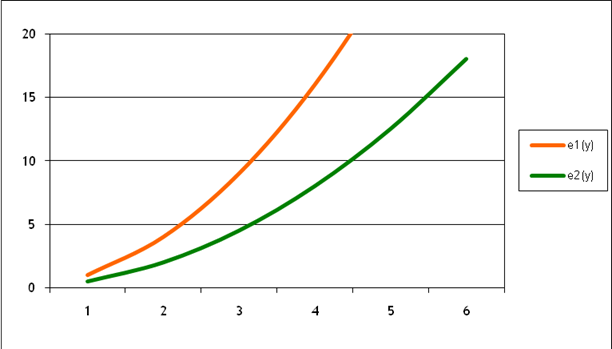
If emissions of each firm are 16, then firm 1 is producing 4 units of electricity while firm 2 is producing 5.66 units of electricity. If firm 2 produced one more unit of electricity its emissions would rise to 22.16, an increase of 6.16. If firm 1 produced one less unit of electricity its emissions would fall to 9, a decrease of 7. So if, instead of both firms producing 16 units of emissions, firm 1 produced less and firm 2 produced more, the overall production of electricity could remain constant while emissions fall.

We can continue this trade-off as long as the marginal rates of transformation are unequal. It is only when the marginal rates of transformation are equal that there will be a total efficient way of getting the most output with the least amount of harmful emissions.

With a bit more math, we can find the point where the MRTs for each firm will be equal.

Multiple Inputs

It is rarely quite appropriate to consider an output to be perfectly free, since there are usually at least technological considerations. So we can return to our usual marginal conditions, modified for the firm. Consider a firm which has multiple inputs available for making the output, each of which is useful and productive. Each input has a cost (or wage, if we extrapolate from the case of hiring workers) denoted w_i.

We typically assume that, holding all of the other inputs constant, increases to just one input will have a steadily-decreasing effect on increasing output. Graphically, this says that for each input, x_i, i=1, 2, … N, output, y, increases as:

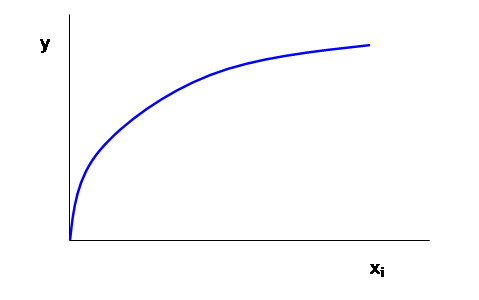
So, just as with the consumer's diminishing marginal utility, the firm faces diminishing marginal productivity. Just as with the consumer, we define the production function as and the marginal product of each input as the partial derivative, .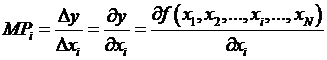

Also as noted previously, the fact that each individual marginal product is diminishing does not mean that production overall has diminishing returns to scale – where 'scale' refers to a case where all of the relevant inputs are increased. As a simple example, most offices generally operate with each employee getting a computer. Buying more computers without hiring more people might increase output, but at a diminishing rate; the same would hold true for hiring more people without getting more computers. But getting more of both could allow the business to expand.

The firm will maximize profits by choosing inputs such that (in the long run), the ratios of , marginal productivity per cost of each input, is equal. The explanation should, by now, be typical: if spending $1 more on input i increased output by more than spending $1 more on input j, then the firm should decrease spending on input i while increasing spending on input j. This will not only allow the firm to make more output more cheaply but also tend to bring down the marginal productivity of input j while increasing the marginal productivity of input i, so that in equilibrium we have .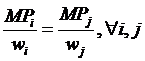

If one input has a price which is increased (say, by some environmental regulation) then this input will be used less. This is the substitution effect (see from marginal condition).

There is also a Scale Effect. As the cost of production rises, the quantity of output demanded will fall, so fewer of all types of input will be demanded.

Also, if that input is non-excludable like polluted air or water, then other industries could see their costs fall, so input used more – a different substitution effect. Also a different scale effect.

Hicks-Marshall rules of Derived Demand:

Demand for input is more elastic when

1. technical substitution is easy

2. input cost share is high

3. input substitutes are supplied elastically

4. demand for output is elastic

Social Welfare

It is difficult enough to figure out how some impartial policy analyst might discover these when social marginal cost or social marginal willingness to pay differs from the private analogs, or what tax/subsidy would cure it. But that presumes that policymakers want to maximize social surplus. To what extent is that a good assumption?

First, how exactly do we (ought we) define Sustainability?

Sustainability and Sustainable Development

Principal definition from the 1987 Brundtland Commission, Sustainable Development is development that meets the needs of present generations without compromising the ability of future generations to meet their own needs.

At the American Museum of Natural History here in New York, the entrance rotunda has the following words carved into the wall:

Nature

There is a delight in the hardy life of the open.

There are no words that can tell the hidden spirit of the wilderness, that can reveal its mystery, its melancholy and its charm.

The nation behaves well if it treats the natural resources as assets which it must turn over to the next generation increased; and not impaired in value.

Conservation means development as much as it does protection.

Theodore Roosevelt, 26^th President of the United States (and the youngest ever) and also a winner of Nobel Peace Prize, was a prominent advocate of conservation, wilderness, and the AMNH. The last two sentences can be seen as inconsistent and different varieties of "sustainability" highlight one meaning or the other.

But Teddy Roosevelt's further quotes reveal what he meant, "Conservation means development as much as it does protection. I recognize the right and duty of this generation to develop and use the natural resources of our land; but I do not recognize the right to waste them, or to rob, by wasteful use, the generations that come after us."

"Defenders of the short-sighted men who in their greed and selfishness will, if permitted, rob our country of half its charm by their reckless extermination of all useful and beautiful wild things sometimes seek to champion them by saying the 'the game belongs to the people.' So it does; and not merely to the people now alive, but to the unborn people. The 'greatest good for the greatest number' applies to the number within the womb of time, compared to which those now alive form but an insignificant fraction. Our duty to the whole, including the unborn generations, bids us restrain an unprincipled present-day minority from wasting the heritage of these unborn generations. The movement for the conservation of wild life and the larger movement for the conservation of all our natural resources are essentially democratic in spirit, purpose, and method." (Again, TR, A Book-Lover's Holidays in the Open, 1916.)

Sustainability, in whatever conception, is not straightforward to analyze within an economic framework. We need to work out the details of the definition farther.

From J.C.V. Pezzey & M.A. Toman, (2008) "Sustainability and its Economic Interpretations," draft chapter in Scarcity & Growth in the New Millenium, ed R.U. Ayres, D. Simpson, & M.A. Toman.

Big question: can economy grow forever?

Sustainability in general is about equity between generations. Could either define it as equity of outcomes (utility) or equity of opportunities. If look at outcome, then ask: can future generations' utility continue without declining? If look at opportunity, then does wealth never decline?

Economic problem: in many analyses we assume that people discount the future – find the present discounted value of costs & benefits. We do this in analyzing investments by private companies as well as governments. But this discounting means that the welfare of future generations may not be highly valued.

Early papers on economic growth provide boundaries of the problem. If there is a depletable natural resource, then rational choice (discounting the future) by current generations implies declining consumption over time. If, on the other hand, technological growth is rapid enough, then the discounting dilemma is solved: consumption can grow over time. The discounting dilemma shows that, even if there are no externalities and every good is 'properly' priced, the economy might still be unsustainable.

First question: so what? If every current person likes the unsustainable path, then is there a moral basis to limit current choice? If so, who will limit current choices? Can we distinguish between people acting as 'homo economicus' in markets but as 'Good Citizen' in government? For a good review of how important is economic growth to basic human welfare watch Hans Rosling's TED talk.

Do people act rationally anyway? Do they discount in that way? How do we deal with the uncertainty inherent in some of these models? No easy answers.

Define "Total Capital" as man-made capital (machines) plus human capital (knowledge and expertise) plus natural capital (from the ecosystem). Write

.

Often distinguish between "strong" and "weak" sustainability

- weak sustainability implies that total capital does not decline – but this can include cases where natural capital is used to increase human or man-made capital. This assumes that each type of capital is a perfect substitute for the other. Also assumes that there is some metric to convert all of the types of capital into a single unit (usually present-value money) – otherwise how to add up machinery and university degrees with coal fields, biodiversity, and clean water?

- strong sustainability implies that at least some component of K_N cannot fall below some critical value – there are threshold effects. Precautionary Principle follows. The Stern Report on Climate Change ended up using this sort of argument to overcome the disagreements about measurement that are inherent in the previous definition.

- Green Net National Product (GNNP) proposed to supplement GNP to offset the depreciation of K_Natural. Augmented National Income takes Green but adds in technological progress. Related is Genuine Savings, which gives net investment after depreciation of all of the capital amounts. So if Augmented National Income is not rising then economy is unsustainable.

- if economy has endogenous growth then this might be fast enough to overcome environmental degradation

- Other measures include "carbon footprint" (or other footprints) but these lack clear justification

Fundamental question: if future generations will be much richer, then why must we now sacrifice for them? Why should the poor (us today) give to the rich (future generations)? Many countries and societies have developed by first exploiting natural resources to get rich, then only later remediating environmental harm (e.g. the USA).

This question of discounting arises often in policy disputes. We will come back to it (esp. in climate change) but for now note that there is no simple answer.

Social Welfare

How can we, as economists, say much about which outcomes are better than others, without imposing our own particular ethics and morals? Some outcomes might deliver high income inequality; some might constrain inequality but with a lower average level of consumption. How can we say which is better?

I'll use the general term "government" but this refers to any joint decision making body. People get together to form various organizations, which then promulgate rules that bind the members – any of these organizations can be considered a 'government' from the view of social welfare analysis. A building coop is a 'government' of a sort: it makes rules that (hopefully) help the people who live there. Business Improvement Districts join up local merchants. There are unions and farmer marketing boards. Then there are myriad levels of government in the conventional sense of the word.

So how can a government choose its goals? One of the very minimal items that we might propose, is that we ought not to omit any movements in allocations that are "Pareto improving." A Pareto improving trade gives something for nothing – someone gets more utility without anyone else getting less utility. Certainly these sorts of trades ought to be made, right? So a "Pareto optimal" economy has eliminated all of these possible trades and has no more possibility of getting something for nothing.

This is what kids do after getting Halloween candy: the one who likes chocolate best will trade away the Starbursts and gummi bears to friends who like those more than chocolate. Everyone wins.

The First Welfare Theorem of Economics tells that every (frictionless) market equilibrium is Pareto optimal. This tells us that, based on the rather meager definition of "optimal" that we just gave, that each market equilibrium meets this low criterion. This is nearly by definition: if there were some trade that would make both parties happier, then they would make it in a market economy (unless constrained by some friction; e.g. the whole Coase discussion).

The Second Welfare Theorem of Economics is more interesting. We just said that "Pareto optimal" is a weak condition – a dictatorship where one person has nearly all of the wealth, while the others toil in peonage, could be Pareto optimal. There are many possible Pareto optimal equilibria. Suppose society had some idea of which particular one it wanted – could a market economy get us there? The Second Welfare Theorem tells that every Pareto optimal allocation is a market equilibrium that started from some initial endowment. So this makes a lovely separation: if policymakers want to change which allocation they desire, then they ought to change the initial endowments. The market system is not the reason for inequalities or injustices – these mirror inequities in the original allocations.

But, as we said, there are many Pareto Optimal allocations – this is one consideration but not the sole consideration. How can society choose the "best" outcome? The Second Welfare Theorem said that, if we had something to aim for, we know how to hit it. But what do we aim for?

Not every Pareto Optimal allocation is very good: if we start from an aristocratic society with 1% of people getting nearly all of the wealth while the other 99% live at subsistence level, then there is no Pareto improvement that will help the 99% who are peasants without taking something away from the aristocrats.

We would like to have some sort of society utility function, analogous to an individual utility function, so that we could use the rational choice apparatus to look at social choices. Call this a "Social Welfare Function," denoted W( ).

One idea for a Social Welfare function is Utilitarianism, originally due to Jeremy Bentham, which holds that we should just add up the utilities of the people in the society, u₁, … u_N. This sets

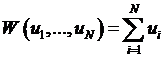, or, with slightly more generality,

,

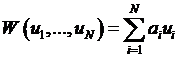where the a_i are weights. This has problems, chiefly being the impossibility of measurement, then the impositions upon human rights.

Remember from our definitions of utility functions that these are just arbitrary functions which represent preferences; any monotonically increasing function of a utility function is itself a utility function. One person's utility of chocolate could be 1,000,000,000; another's could be -1 but we CANNOT conclude that the first person likes chocolate better. How can we compare happiness levels?

Then there is the problem of human rights: if we believe that people have "certain inalienable rights" then the utilitarian framework could justify, say, selling one person into slavery if the money raised can make others happy enough.

The philosopher John Rawls proposed a minimax function,

.

He propelled this function by arguing that most people's definitions of a fair allocation depend upon their knowledge of their own situation: someone who is intelligent might happily agree to a society where smart people are well rewarded; someone else with different advantages would argue for a different allocation. He proposed a thought experiment: what allocation would be chosen, if the members of society could get together before they knew what their own situation would be – whether they would be fortunate or unlucky, healthy or sick, endowed with which talents? They would have to make a decision from behind a "veil of ignorance" over their future endowments. Rawls argued that, from this perspective, a person would give a great weight to the worst possibility – extreme risk aversion – that a society with substantial inequality would not be appealing because even a small chance of being utterly destitute would be too large. Therefore he proposed a minimax principle, that every change in allocation, away from perfect equality, must help the worst-off person. So he would allow greater rewards to, say, doctors, in order to give them incentive to help the sick and the most fragile members of society.

These social welfare functions so far allow people's utilities to depend on anything and everything. We might further restrict that people's utilities depend only on their own consumptions, in which case we would have a Bergson-Samuelson welfare function. But this is not generally realistic.

Rights-based social welfare functions run into difficulties since these generally do not allow tradeoffs – a slight diminution in some right might make everyone better off. But rights-based are generally "lexicographic" preferences where no positive benefit can possibly compensate ("lexicographic" since Azzz is alphabetized before Baaa). Yet different people have different ideas about which rights are most important (in the US, the Supreme Court must adjudicate when there are competing rights clashing). Many people voluntarily surrender certain rights in order to gain other benefits (e.g. a coop or condo association restricts property rights but is beneficial to property values); it is unclear why a social welfare function should not do so.

We might hope for an answer like "democracy". But Ken Arrow (CCNY alumnus and Nobel Prize winner) showed that a democracy does not guarantee rational orderings of choices.

Arrow's Theorem states that if we desire:

1. Completeness: The social welfare function, W( ), is defined for all allocations,
2. The social welfare function is responsive to individual preferences,
3. It is independent of irrelevant alternatives (so if W(X)>W(Y) then adding a choice Z, if W(X)>W(Z), does not change the original ordering) (like Transitivity)
4. It is not an imposed dictatorship.

Then, if there are more than 3 choices, there is NO POSSIBLE Social Welfare function can be guaranteed to satisfy all four conditions.

People care about justice and fairness and other considerations. Too many policy debates result from arguing about proposals, where each side uses radically different definitions of these terms – what do justice and fairness mean? Economists have proposed some definitions.

The Second Welfare Theorem got us focused upon initial allocations, so we might wonder if that will help. Is a symmetric distribution, where everyone gets exactly the same bundle of goods, fair? If people's utility functions are not perfectly uniform then people will voluntarily trade among themselves, and we will move away from perfect equality. Is this desirable? Would someone envy another person's allocation? Define envy that person i would prefer j's bundle rather than her own. An allocation is equitable if none of the bundles are envied. Define a fair allocation as one that is equitable and Pareto efficient (i.e. nothing is wasted). Now it can be proved that if society starts from a symmetric distribution then the outcome of market trading will be fair, under this definition. (But the symmetric outcome is not generally fair.)

From the definitions of Pareto optimality, economists have often backed off to the measure, "Possibly Pareto Improving" (or Potentially Pareto Improving), to indicate that some policy could generate enough surplus to compensate the losers and still leave the winners with something. For example, a policy that gave A $100 while costing B just $40 would be Possibly Pareto Improving since A could compensate B the $40 lost and A would still be $60 ahead. This is the theory behind the general introductory lesson on Deadweight Loss (DWL) – that social surplus could be increased by enough to compensate the losers and still leave the winners ahead.

This sneaks back a bit of Utilitarianism into the argument – now we're comparing utilities but using the measure of dollars (marginal willingness to pay).

The problem with "Possibly Pareto Improving" policies is obvious: the "Possible" does not mean that it actually does occur! A policy that made Bill Gates $100 wealthier while making the poorest person $90 poorer would likely be condemned by a variety of social welfare functions. But it is "Possibly Pareto Improving" (even if it is improbable that it actually will be). Policymakers could justify a progressive tax on the theory that it distributes some of these Possible Pareto gains from the winners to the losers, but the connection between this progressive tax and other policies is often lost.

The typical economist's tool of "Cost-Benefit Analysis" has this same shortcoming. This would add up the marginal costs of some policy, add up the marginal benefits, and then make the change if the benefits outweighed the costs. Again this avoids all questions of who gets the net (social) profit! Cost-Benefit Analysis is the same as Possible Pareto Improving.