|
Lecture Notes 4 Econ 29000, Principles of Statistics Kevin R Foster, CCNY Spring 2012 |
|
|
|
Discrete Random Variables |
|
|
For any discrete random variable, the mean or expected value is:
and the variance is
so the standard deviation is the square root.
Can be described by PDF or CDF. The PDF shows the probability of events; the CDF shows the cumulative probability of an event that is smaller than or equal to that event.
Linear Transformations:
· If then Y will have mean and standard deviation .
· If then ; (and if X and Y are independent then the covariance term drops out)
WARNING: These statements DO NOT work for non-linear calculations! The propositions above do NOT tell about when X and Y are multiplied and divided: the distributions of or are not easily found. Nor is , nor . We might wish for a magic wand to make these work out simply but they don't in general.
Common Discrete Distributions:
Uniform
· depend on only upper and lower bound, so all events are in
· mean is ; standard deviation is
· Excel's random number generator (=RAND()) gives a uniform distribution in [0,1]
· Many null hypotheses are naturally formulated as stating that some distribution is uniform: e.g. stock picks, names and grades, birth month and sports success, etc.
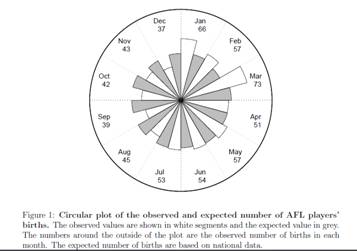
from: Barnett, Adrian G. (2010) The relative age effect in Australian Football League players. Working Paper.
Benford's Law: not really a law but an empirical result about measurements, that looking at the first digit, the value 1 is much more common than 9 – the first digit is not uniformly distributed. Originally stated for tables of logarithms. Second digit is closer to uniform; third digit closer still, etc. See online Excel sheet.
Bernoulli
· depend only on p, the probability of the event occurring
· mean is p; standard deviation is
o Where is max? Intuition: what probability will give the most variation in yes/no answers? Or use calculus; note that has same maximum as p(1 – p) so take derivative of that, set to zero
· for coin flips, dice rolls, events with "yes/no" answers: Was person re-employed after layoff? Did patient improve after taking the drug? Did company pay out to investors from IPO?
· in Excel, to get a zero or one, where a one has a 0.44 probability, the formula would be =IF(RAND()<0.44,1,0) [note that this is unchanged by whether you use "<" or "<="]
Binomial
· have n Bernoulli trials; record how many were 1 not zero
· ;
o These formulas are easy to derive from rules of linear combinations. If Bi are independent random variables with Bernoulli distributions, then what is the mean of B1 + B2? What is its std dev?
o What if this is expressed as a fraction of trials? Derive.
· what fraction of coin flips came up heads? What fraction of people were re-employed after layoff? What fraction of patients improved? What fraction of companies offereed IPOs?
· questions about opinion polls – the famous "plus or minus 2 percentage points"
o get margin of error depending on sample size (n)
o from above, figure that mean of the fraction of people who agree or support some candidate is p, the true value, with standard error of .
Some students are a bit puzzled by two different sets of formulas for the binomial distribution – the standard deviation is listed as and . Which is it?!
It depends on the units. If we measure the number of successes in n trials, then we multiply by n. If we measure the fraction of successes in n trials, then we don't multiply but divide.
Consider a simple example: the probability of a hit is 50% so . If we have 10 trials and ask, how many are likely to hit, then this should be a different number than if we had 500 trials. The standard error of the raw number of how many, of 10, hits we would expect to see, is which is 1.58, so with a 95% probability we would expect to see 5 hits, plus or minus 1.96*1.58 = 3.1 so a range between 2 and 8. If we had 500 trials then the raw number we'd expect to see is 250 with a standard error or = 11.18 so the 95% confidence interval is 250 plus or minus 22 so the range between 228 and 272. This is a bigger range (in absolute value) but a smaller part of the fraction of hits.
With 10 draws, we just figured out that the range of hits is (in fractions) from 0.2 to 0.8. With 500 draws, the range is from 0.456 to 0.544 – much narrower. We can get these latter answers if we take the earlier result of standard deviations and divide by n. The difference in the formula is just this result, since . You could think of this as being analogous to the other "standard error of the average" formulas we learned, where you take the standard deviation of the original sample and divide by the square root of n.
Poisson
· model arrivals per time, assuming independent
· depends only on which is also mean
· PDF is
· model how long each line at grocery store is, how cars enter traffic, how many insurance claims
Example of a very simple model (too simple)
Use computer to create models of stock price movements. What model? How complicated is "enough"?
Start really simple: Suppose the price were 100 today, and then each day thereafter it rises/falls by 10 basis points. What is the distribution of possible stock prices, after a year (250 trading days)?
|
Use Excel (not even SPSS for now!)
First, set the initial price at 100; enter 100 into cell B2 (leaves room for labels). Put the trading day number into column A, from 1 to 250 (shortcut). In B1 put the label, "S".
Then label column C as "up" and in C2 type the following formula, =IF( The "
Then label column D as "down" and in D2 just type =1-C2 Which simply makes it zero if "up" is 1 and 1 if "up" is 0.
Then, in B3, put in the following formula, =B2*(1+0.001*(C2-D2))
Copy and paste these into the remaining cells down to 250.
Of course this isn't very realistic but it's a start.
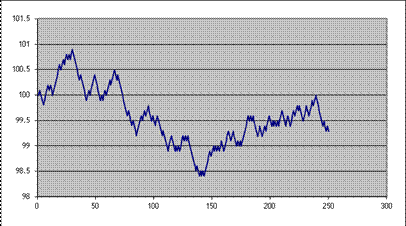
Then plot the result (highlight columns A&B, then "Insert\Chart\XY (Scatter)"); here's one of mine:
|
|
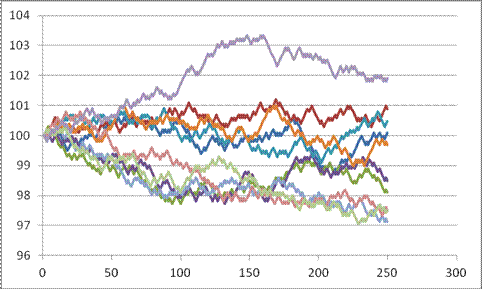
Here are 10 series (copied and pasted the whole S, "up," and "down" 10 times), see Excel sheet "Lecturenotes4".
|
We're not done yet; we can make it better. But the real point for now is to see the basic principle of the thing: we can simulate stock price paths as random trips.
The changes each day are still too regular – each day is 10 bps up or down; never constant, never bigger or smaller. That's not a great model for the middle parts. But the regularity within each individual series does not necessarily mean that the final prices (at step 250) are all that unrealistic.
I ran 2000 simulations; this is a histogram of the final price of the stock:
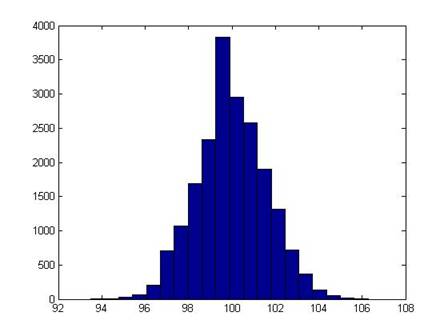
It shouldn't be a surprise that it looks rather normal (it is the result of a series of Bernoulli trials – that's what the Law of Large Numbers says should happen!).
With computing power being so cheap (those 2000 simulations of 250 steps took a few seconds) these sorts of models are very popular (in their more sophisticated versions).
It might seem more "realistic" if we thought of each of the 250 tics as being a portion of a day. ("Realistic" is a relative term; there's a joke that economists, like artists, tend to fall in love with their models.)
There are times (in finance for some option pricing models) when even this very simple model can be useful, because the fixed-size jump allows us to keep track of all of the possible evolutions of the price.
But clearly it's important to understand Bernoulli trials summing to Binomial distributions converging to normal distributions.
|
Continuous Random Variables |
|
|
The PDF and CDF
Where discrete random variables would sum up probabilities for the individual outcomes, continuous random variables necessitate some more complicated math. When X is a continuous random variable, the probability of it being equal to any particular value is zero If X is continuous, there is a zero chance that it will be, say, 5 – it could be 4.99998 or 5.000001 and so on. But we can still take the area under the PDF by taking the limit of the sum, as the horizontal increments get smaller and smaller – the Riemann method, for those who remember Calculus. So to find the probability of X being equal to a set of values we integrate the PDF between those values, so
.
The CDF, the probability of observing a value less than some parameter, is therefore the integral with as the lower limit of integration, so .
For this class you aren't required to use calculus but it's helpful to see why somebody might want to use it. (Note that many of the statistical distributions we'll talk about come up in solving partial differential equations such as are commonly used in finance – so if you're thinking of a career in that direction, you'll want even more math!)
Normal Distribution
We will most often use the Normal Distribution – but usually the first question from students is "Why is that crazy thing normal?!!" You're not the only one to ask
In statistics it is often convenient to use a normal distribution, the bell-shaped distribution that arises in many circumstances. It is useful because the (properly scaled) mean of independent random draws of many other statistical distributions will tend toward a normal distribution – this is the Central Limit Theorem.
Some basic facts and notation: a normal distribution with mean µ and standard deviation s is denoted N(µ,s). (The variance is the square of the standard deviation, s2.) The Standard Normal distribution is when µ=0 and s=1; its probability density function (pdf) is denoted pdfN(x); the cumulative density function (CDF) is cdfN(x) or sometimes Nor(x). This is a graph of the PDF (the height at any point) and CDF of the normal:
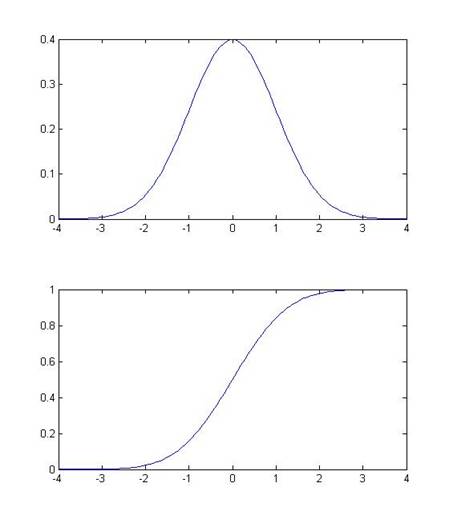
One of the basic properties of the normal distribution is that, if X is distributed normally with mean µ and standard deviation s, then Y = A + bX is also distributed normally, with mean (A + bµ) and standard deviation bs. We will use this particularly when we "standardize" a sample: by subtracting its mean and dividing by its standard deviation, the result should be distributed with mean zero and standard deviation 1.
Oppositely, if we are creating random variables with a
standard deviation, we can take random numbers with a N(0,1) distribution,
multiply by the desired standard deviation, and add the desired mean, to get
normal random numbers with any mean or standard deviation. In Excel, you can create normally distributed
random numbers by using the RAND()
function to generate uniform random numbers on [0,1], then NORMSINV(
Motivation: Sample Averages are Normally Distributed
Before we do a long section on how to find areas under the normal distribution, I want to address the big question: Why we the heck would anybody ever want to know those?!?!
Consider a case where we have a population of people and we sample just a few to calculate an average. Before elections we hear about these types of procedures all of the time: a poll that samples just 1000 people is used to give information about how a population of millions of people will vote. These polls are usually given with a margin of error ("54% of people liked Candidate A over B, with a margin of error of plus or minus 2 percentage points"). If you don't know statistics then polls probably seem like magic. If you do know statistics then polls are based on a few simple formulas.
I have a dataset of about 206,639 people who reported their wage and salary to a particular government survey, the "Current Population Survey," the CPS. The true average of their wage and salaries was $19,362.62. (Not quite; the top income value is cut at $625,000 – people who made more are still just coded with that amount. But don't worry about that for now.) The standard deviation of the full 206,639 people is 39,971.91.
A histogram of the data shows that most people report zero (zero is the median value), which is reasonable since many of them are children or retired people. However some report incomes up to $625,000!
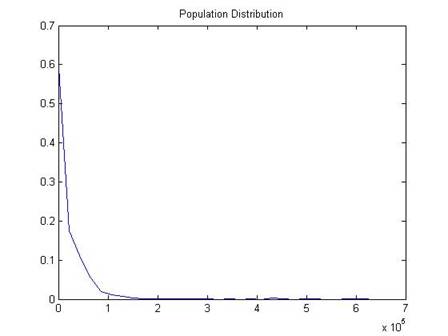
Taking an average of a population with such extreme values would seem to be difficult.
Suppose that I didn't want to calculate an average for all 206,639 people – I'm lazy or I've got a real old and slow computer or whatever. I want to randomly choose just 100 people and calculate the sample average. Would that be "good enough"?
Of course the first question is "good enough for what?" – what are we planning to do with the information?
But we can still ask whether the answer will be very close to the true value. In this case we know the true value; in most cases we won't. But this allows us to take a look at how the sampling works.
Here is a plot of values for 1000 different polls (each poll with just 100 people).
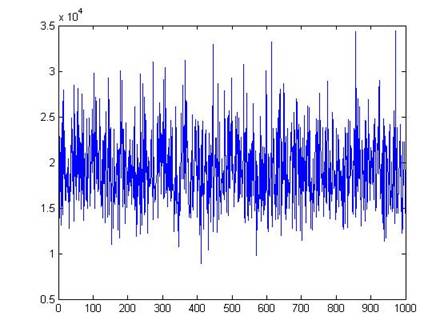
We can see that, although there are a few polls with averages as low almost 10,000 and a few with averages as high as 30,000, most of the polls are close to the true mean of $19,363.
In general the average of even a small sample is a good estimate of the true average value of the population. While a sample might pick up some extreme values from one side, it is also likely to pick extreme values from the other side, which will tend to balance out.
A histogram of the 1000 poll means is here:
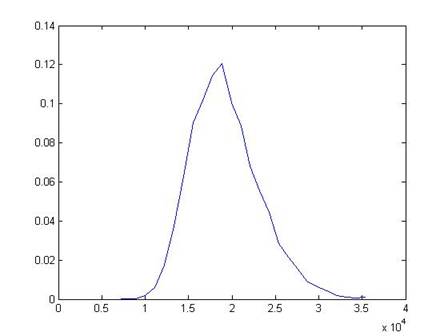
This shows that the distribution of the sample means looks like a Normal distribution – another case of how "normal" and ordinary the Normal distribution is.
Of course the size of each sample, the number of people in each poll, is also important. Sampling more people gets us better estimates of the true mean.
This graph shows the results from 100 polls, each with different sample sizes.
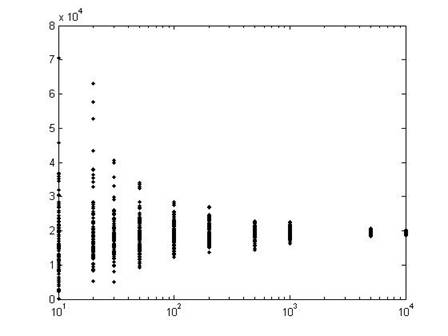
In the first set of 100 polls, on the left, each poll has just 10 people in it, so the results are quite varied. The next set has 20 people in each poll, so the results are closer to the true mean. By the time we get to 100 people in each poll (102 on the log-scale x-axis), the variation in the polls is much smaller.
Each distribution has a bell shape, but we have to figure out if there is a single invariant distribution or only a family of related bell-shaped curves.
If we subtract the mean, then we can center the distribution around zero, with positive and negative values indicating distance from the center. But that still leaves us with different scalings: as the graph above shows, the typical distance from the center gets smaller. So we divide by its standard deviation and we get a "Standard Normal" distribution.
The Standard Normal graph is:
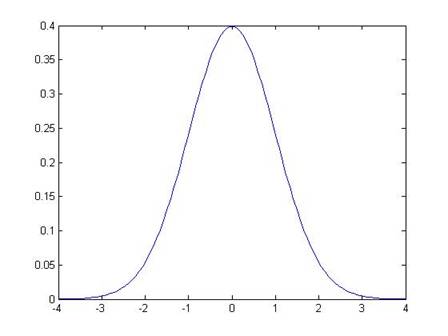
Note that it is symmetric around zero. Like any histogram, the area beneath the curve is a measure of the probability. The total area under the curve is exactly 1 (probabilities must add up to 100%). We can use the known function to calculate that the area under the curve, from -1 to 1, is 68.2689%. This means that just over 68% of the time, I will draw a value from within 1 standard deviation of the center. The area of the curve from -2 to 2 is 95.44997%, so we'll be within 2 standard deviations over 95.45% of the time.
It is important to be able to calculate areas under the Standard Normal. For this reason people used to use big tables (statistics textbooks still have them); now we use computers. But even the computers don't always quite give us the answer that we want, we have to be a bit savvy.
So the normal CDF of, say, -1, is the area under the pdf of the points to the left of -1:
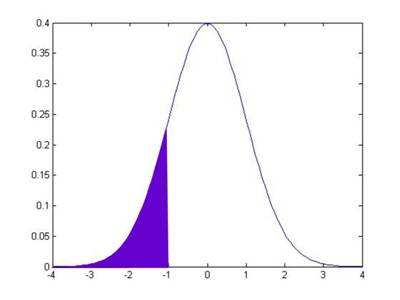
This area is 15.87%. How can I use this information to get the value that I earlier told you, that the area in between -1 and 1 is 68.2689%? Well, we know two other things (more precisely, I know them and I wrote them just 3 paragraphs up, so you ought to know them). We know that the total area under the pdf is 100%. And we know that the pdf is symmetric around zero. This symmetry means that the area under the other tail, the area from +1 all the way to the right, is also 15.87%.
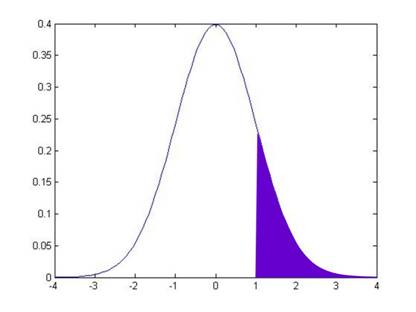
So to find the area in between -1 and +1, I take 100% and subtract off the two tail areas:
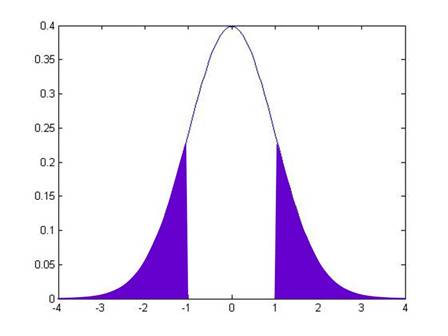
And this middle area is 100 – 15.87 – 15.87 = 68.26.
Sidebar: you can think of all of this as "adding up" without calculus. On the other hand, calculus makes this procedure much easier and we can precisely define the cdf as the integral, from negative infinity to some point Z, under the pdf: .
So with just this simple knowledge, you can calculate all sorts of areas using just the information in the CDF.
Hints on using Excel,
SPSS, and Matlab to calculate the Standard
Excel
Excel has both normdist and normsdist. For normdist, you need to tell it the mean and standard deviation, so use the function normdist(X,mean,stdev,cumulative). For normsdist it assumes the mean is zero and standard deviation is one so you just use normsdist(X). Read the help files to learn more. The final argument of the normdist function, "Cumulative" is a true/false: if true then it calculates the cdf (area to the left of X); if false it calculates the pdf. [Personally, that's an ugly and non-intuitive bit of coding, but then again, Microsoft has no sense of beauty.]
To figure out the other way – what X value gives me some particular probability, we use norminv or normsinv.
All of these commands are under "Insert" then "Function" then, under "Select a Category" choose "Statistical".
SPSS
For SPSS you can open it up with an empty dataset and go to the "Data View" tab. Then use "Transform," "Compute Variable…" and, under "Function Group" find "CDF and Noncentral CDF". Then "Cdf.Normal(X,mean,stdev)" calculates the normal cdf for the given X variable. Select this function and use the up-arrow to push it into the "Numeric Expression" dialog box. For any of the inputs (which SPSS denotes as "?") you can click on a variable from the list on the left. Or just type in the values. You need to give your output variable a name, this is the blank "Target Variable" on the upper left-hand side. If you're just doing calculations then give it any name; later on, if you are doing more complex series of calculations, you can worry about understandable variable names. Then hit "OK" and look back in the "Data View." (It will spawn an Output view but that only tells you if there were errors in the function.)
To go backwards, find "Inverse DF" under "Function Group" and then "IDF.Normal(p,mean,stdev)" where you input the probability.
Matlab
Matlab has the command, normcdf(X,mean,stdev). The inputs mean and stdev are the mean and standard deviations of the normal distribution considered; for the Standard Normal you can just leave those blank and just write normcdf(X). If X is a vector or matrix then it computes the standard normal cdf of each cell value. The function normpdf(X,mean,stdev) is the pdf naturally.
Norminv(p,mean,stdev) gives the inverse of the normcdf function and normsinv(p) gives the inverse for the standard normal.
Side Note: The basic property, that the distribution is normal whatever the time interval, is what makes the normal distribution {and related functions, called Lévy distributions} special. Most distributions would not have this property so daily changes could have different distributions than weekly, monthly, quarterly, yearly, or whatever!
Recall from calculus the idea that some functions are not differentiable in places – they take a turn that is so sharp that, if we were to approximate the slope of the function coming at it from right or left, we would get very different answers. The function, , is an example: at zero the left-hand derivative is -1; the right-hand derivative is 1. It is not differentiable at zero – it turns so sharply that it cannot be well approximated by local values. But it is continuous – it can be continuous even if it is not differentiable.
Now suppose I had a function that was everywhere continuous but nowhere differentiable – at every point it turns so sharply as to be unpredictable given past values. Various such functions have been derived by mathematicians, who call it a Wiener process (it generates Brownian motion). (When Einstein visited CCNY in 1905 he discussed his paper using Brownian motion to explain the movements of tiny particles in water, that are randomly bumped around by water molecules.) This function has many interesting properties – including an important link with the Normal distribution. The Normal distribution gives just the right degree of variation to allow continuity – other distributions would not be continuous or would have infinite variance.
Note also that a Wiener process has geometric form that is independent of scale or orientation – a Wiener process showing each day in the year cannot be distinguished from a Wiener process showing each minute in another time frame. As we noted above, price changes for any time interval are normal, whether the interval is minutely, daily, yearly, or whatever. These are fractals, curious beasts described by mathematicians such as Mandelbrot, because normal variables added together are still normal. (You can read Mandelbrot's 1963 paper in the Journal of Business, which you can download from JStor – he argues that Wiener processes are unrealistic for modeling financial returns and proposes further generalizations.)
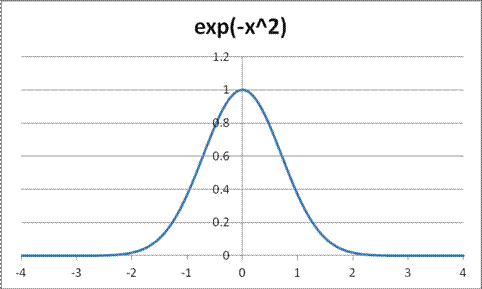
The Normal distribution has a pdf which looks ugly but isn't so bad once you break it down. It is proportional to . This is what gives it a bell shape:
To make this a real probability we need to have all of its area sum up to one, so the probability density function (PDF) for a standard normal (with zero mean and standard deviation of one) is
.
To allow a mean, µ, different from zero and a standard deviation, σ, different from one, we modify the formula to this:
.
The connection with e is useful if it reminds you of when you learned about "natural logarithms" and probably thought "what the heck is 'natural' about that ugly thing?!" But you learn that it comes up everywhere (think it's bad now? wait for differential equations!) and eventually make your peace with it. So too the 'normal' distribution.
If you think that the PDF is ugly then don't feel bad – its discoverer didn't like it either. Stigler's History of Statistics relates that Laplace first derived the function as the limit of a binomial distribution as but couldn't believe that anything so ugly could be true. So he put it away into a drawer until later when Gauss derived the same formula (from a different exercise) – which is why the Normal distribution is often referred to as "Gaussian". The Normal distribution arises in all sorts of other cases: solutions to partial differential equations; in physics Maxwell used it to describe the diffusion of gases or heat (again Brownian motion); in information theory where it is connected to standard measures of entropy (Kullback Liebler); even in the distribution of prime factors in number theory, the Erdős–Kac Theorem.
Finally I'll note the statistical quincunx, which is a great word since it sounds naughty but is actually geeky (google it or I'll try to get an online version to play in class).