|
Lecture Notes 8 Econ 20150, Principles of Statistics Kevin R Foster, CCNY Spring 2012 |
|
|
|
Details of Distributions T-distributions, chi-squared, etc. |
|
|
Take the basic methodology of Hypothesis Testing and figure out how to deal with a few complications.
T-tests
The first complication is if we have a small sample and we're estimating the standard deviation. In every previous example, we used a large sample. For a small sample, the estimation of the standard error introduces some additional noise – we're forming a hypothesis test based on an estimation of the mean, using an estimation of the standard error.
How "big" should a "big" sample be? Evidently if we can easily get more data then we should use it, but there are many cases where we need to make a decision based on limited information – there just might not be that many observations. Generally after about 30 observations is enough to justify the normal distribution. With fewer observations we use a t-distribution.
To work with t-distributions we need the concept of "Degrees of Freedom" (df). This just takes account of the fact that, to estimate the sample standard deviation, we need to first estimate the sample average, since the standard deviation uses . So we don't have as many "free" observations. You might remember from algebra that to solve for 2 variables you need at least two equations, three equations for three variables, etc. If we have 5 observations then we can only estimate at most five unknown variables such as the mean and standard deviation. And "degrees of freedom" counts these down.
If we have thousands of observations then we don't really need to worry. But when we have small samples and we're estimating a relatively large number of parameters, we count degrees of freedom.
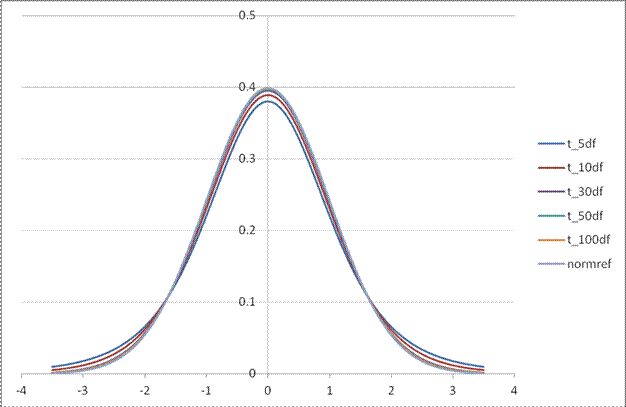
The family of t-distributions with mean of zero looks basically like a Standard Normal distribution with a familiar bell shape, but with slightly fatter tails. There is a family of t-distributions with exact shape depending on the degrees of freedom; lower degrees of freedom correspond with fatter tails (more variation; more probability of seeing larger differences from zero).
This chart compares the Standard Normal PDF with the t-distributions with different degrees of freedom.
This table shows the different critical values to use in place of our good old friend 1.96:
|
Critical Values for t vs N |
|
|||||
|
df |
95% |
90% |
99% |
|||
|
5 |
2.57 |
|
2.02 |
|
4.03 |
|
|
10 |
2.23 |
1.81 |
3.17 |
|||
|
20 |
2.09 |
1.72 |
2.85 |
|||
|
30 |
2.04 |
1.70 |
2.75 |
|||
|
50 |
2.01 |
1.68 |
2.68 |
|||
|
100 |
1.98 |
1.66 |
2.63 |
|||
|
Normal |
1.96 |
|
1.64 |
|
2.58 |
|
The higher numbers for lower degrees of freedom mean that the confidence interval must be wider – which should make intuitive sense. With just 5 or 10 observations a 95% confidence interval should be wider than with 1000 or 10,000 observations (even beyond the familiar sqrt(N) term in the standard error of the average).
Note on the t-distribution:
Talk about the t distribution always makes me thirsty. Why? It was originally called "Student's t distribution" because the author wanted to remain anonymous and referred to himself as just a student of statistics. William Gosset worked at Guinness Brewing, which had a policy against its employees publishing material based on their work – they didn't want their brewing secrets revealed! It's amusing to think that Gosset, who graduated top of his class from the one of the world's top universities in 1899, went to work at Guinness –at the time that was a leading industrial company doing cutting-edge research. A half-century later, the brightest students from top universities would go to GM; after a century the preferred destinations would be Google or Goldman Sachs. The only thing those companies have in common is the initial G.
T-tests with two samples
When we're comparing two sample averages we can make either of two assumptions: either the standard deviations are the same (even though we don't know them) or they could be different. Of course it is more conservative to assume that they're different (i.e. don't assume that they're the same) – this makes the test less likely to reject the null.
Assuming that the standard errors are different, we compare this test statistic against a t-distribution with degrees of freedom of the minimum of either or .
Sometimes we have paired data, which can give us more powerful tests.
We can test if the variances are in fact equal, but a series of hypothesis tests can give us questionable results.
Other Distributions
There are other sampling distributions than the Normal Distribution and T-Distribution. There are χ2 (Chi-Squared) Distributions (also characterized by the number of degrees of freedom); there are F-Distributions with two different degrees of freedom. For now we won't worry about these but just note that the basic procedure is the same: calculate a test statistic and compare it to a known distribution to figure out how likely it was, to see the actual value.
(On Car Talk they joked, "I once had to learn the entire Greek alphabet for a college class. I was taking a course in ... Statistics!")
|
Review |
|
|
Take a moment to appreciate the amazing progress we've made: having determined that a sample average has a normal distribution, we are able to make a lot of statements about the probability that various hypotheses are true and about just how precise this measurement is.
What does it mean, "The sample average has a normal distribution"? Now you're getting accustomed to this – means standardize into a Z-score, then lookup against a standard normal table. But just consider how amazing this is. For millennia, humans tried to say something about randomness but couldn't get much farther than, well, anything can happen – randomness is the absence of logical rules; sometimes you flip two heads in a row, sometimes heads and tails – who knows?! People could allege that finding the sample average told something, but that was purely an allegation – unfounded and un-provable, until we had a normal distribution. This normal distribution still lets "anything happen" but now it assigns probabilities; says that some outcomes are more likely than others.
And it's amazing that we can use mathematics to say anything useful about random chance. Humans invented math and thought of it as a window into the unchanging eternal heavens, a glimpse of the mind of some god(s) – the Pythagoreans even made it their religion. Math is eternal and universal and unchanging. How could it possibly say anything useful about random outcomes? But it does! We can write down a mathematical function that describes the normal distribution; this mathematical function allows us to discover a great deal about the world and how it works.
You have doubtless noticed by now that much of the basic statistical reasoning comes down to simply putting the numbers into a basic form, , where the X-bar is the sample average, the Greek letter mu, µ, is the value from the null hypothesis, and the Greek letter sigma, σ, is the standard error of the measurement X-bar. This basic equation was used to transform a variable with a Normal distribution into a variable with a Standard Normal distribution (µ=0 and σ=1) by subtracting the mean and dividing by the standard deviation.
It might not be immediately clear that even when we form hypothesis tests on the differences between two samples A and B, so we compare with , that we're using that same form. But it should be clearer if we notate the difference as D, where , so the test statistic general form is , where we usually test the null hypothesis of µ=0 so it drops out of the equation. The test statistic, , then, is really the usual form, but without writing the zero. Then we use the formula already derived to get the standard error of the difference in means, σD
The only wrinkle introduced by the t-distribution is that we take the exact same form, , but if there are fewer than 30 observations we look up the value in a different table (for a t distribution); if there are more than 30 or so, we look up the value in the normal table just like always.
Going forward, when we use a different estimator (something more sophisticated than the sample average) we will create other test statistics (sometimes called t-statistics) of the same basic form, but for different estimators – call it . Then the test-statistic is , where we use the standard error of this other estimator. So it's not a bad idea, in a beginning course in statistics, to reflexively write down that basic formula and start trying to fill in values. Ask what is the estimator's value in this sample? That's . What is the value of that statistic, if the null hypothesis were true? That's µ. What's the standard error of the estimator? That's . Put those values into the formula and roll!
Statisticians, who know the whole Greek alphabet, sometimes say as "X-wiggle" or "X-twiddle" as if they don't know what a tilde is.