|
Practice for Exam 2 Econ
20150, Principles of Statistics Kevin R Foster, CCNY Spring
2012 |
|
|
Not all of these
questions are strictly relevant; some might require a bit of knowledge that we
haven't covered this year, but they're a generally good guide.
1.
A regression
coefficient is estimated to be equal to 1.205 with standard error 1.3; there
are 22 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.8170 1.6461 0.3640 0.6360
2.
A regression
coefficient is estimated to be equal to -7.986 with standard error 8.1; there
are 4 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.6758 0.8350 0.3800 0.0866
3.
A regression
coefficient is estimated to be equal to 8.703 with standard error 9.3; there
are 26 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.3580 0.7740 0.0752 0.2018
4.
A regression
coefficient is estimated to be equal to 17.535 with standard error 7.5; there
are 6 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.0580 0.1420 0.0000 0.9806
5.
A regression
coefficient is estimated to be equal to -6.496 with standard error 5.6; there
are 10 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.7270 0.8428 0.0753 0.2730
6.
A regression
coefficient is estimated to be equal to 5.797 with standard error 2.3; there
are 17 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.0220 0.1040 0.0978 0.001
7.
A regression
coefficient is estimated to be equal to 3.823 with standard error 3.3; there
are 5 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.0753 0.7010 0.8469 0.2990
8.
A regression
coefficient is estimated to be equal to -2.098 with standard error 1.3; there
are 9 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.1410 0.8590 0.3740 0.9410
9.
A regression
coefficient is estimated to be equal to -7.514 with standard error 5.0; there
are 31 degrees of freedom. What is the p-value (from the t-statistic) against
the null hypothesis of zero? 0.9643 0.0001 0.1430 0.8962
10.
A regression coefficient
is estimated to be equal to 10.965 with standard error 6.1; there are 31
degrees of freedom. What is the p-value (from the t-statistic) against the null
hypothesis of zero? 0.0093 0.2310 0.0820 0.9614
11.
The following
output is from a regression on SPSS with the CPS data; the dependent variable
is "Wages and Salaries". Fill
in the blanks. What is the predicted
wage for a 25-year-old Asian female whose parents were immigrants, with an AS
degree in a vocational field, married, self-employed at an un-incorporated
business?
Coefficientsa |
||||||
|
Model |
Unstandardized
Coefficients |
Standardized
Coefficients |
t |
Sig. |
||
|
B |
Std.
Error |
Beta |
||||
|
1 |
(Constant) |
-25181.864 |
1205.273 |
|
-20.893 |
0 |
|
Demographics, Age |
1858.379 |
65.735 |
0.508 |
__?__ |
__?__ |
|
|
Age squared |
-17.904 |
0.735 |
-0.42 |
__?__ |
__?__ |
|
|
Female |
-14507.904 |
289.657 |
-0.145 |
__?__ |
__?__ |
|
|
African American |
-4493.65 |
444.5 |
-0.029 |
__?__ |
__?__ |
|
|
Asian |
140.766 |
693.136 |
0.001 |
__?__ |
__?__ |
|
|
Native American Indian or Alaskan or Hawaiian |
-3898.462 |
829.529 |
-0.013 |
__?__ |
__?__ |
|
|
Hispanic |
__?__ |
470.854 |
-0.032 |
-9.181 |
0 |
|
|
Immigrant |
__?__ |
610.924 |
-0.055 |
-12.038 |
0 |
|
|
1 or more parents were immigrants |
__?__ |
559.737 |
0.027 |
5.606 |
0 |
|
|
Education: High School Diploma |
__?__ |
507.962 |
0.028 |
6.182 |
0 |
|
|
Education: Some College but no degree |
__?__ |
535.532 |
0.076 |
17.957 |
0 |
|
|
Education: Associate in vocational |
10220.175 |
__?__ |
0.043 |
13.126 |
0 |
|
|
Education: Associate in academic |
13739.167 |
__?__ |
0.062 |
18.371 |
0 |
|
|
Education: 4-yr degree |
27737.896 |
__?__ |
0.223 |
50.275 |
0 |
|
|
Education: Advanced Degree |
54975.701 |
__?__ |
0.34 |
86.69 |
0 |
|
|
Married |
6942.713 |
__?__ |
0.069 |
17.608 |
0 |
|
|
Divorced or Widowed or Separated |
1419.631 |
513.052 |
0.01 |
__?__ |
__?__ |
|
|
Union member |
990.35 |
1022.944 |
0.003 |
__?__ |
__?__ |
|
|
Veteran (any) |
-1434.608 |
576.692 |
-0.007 |
__?__ |
__?__ |
|
|
work for Federal govt |
6740.97 |
821.476 |
0.023 |
__?__ |
__?__ |
|
|
work for state govt |
-10345.286 |
654.328 |
-0.044 |
__?__ |
__?__ |
|
|
work for local govt |
-9641.357 |
526.36 |
-0.052 |
__?__ |
__?__ |
|
|
self employed, incorp |
18190.826 |
745.19 |
0.068 |
__?__ |
__?__ |
|
|
self employed not inc |
-23053.998 |
1415.4 |
-0.045 |
__?__ |
__?__ |
|
|
work without pay |
-4100.955 |
7579.472 |
-0.001 |
__?__ |
__?__ |
|
|
work_fulltime |
18925.467 |
350.572 |
0.163 |
__?__ |
__?__ |
|
|
a. Dependent Variable: Total wage and salary earnings amount –
Person |
||||||
12.
A poll about
people's favorite email provider also asked about political affiliation. They didn't give the original data so I
guessed that it might have looked like the table below.
|
Republicans |
Democrats |
Independents |
|
|
Google |
73 |
121 |
81 |
|
Yahoo |
60 |
113 |
72 |
|
AOL |
78 |
24 |
35 |
|
other |
83 |
59 |
82 |
a.
What fraction of
Republicans listed AOL as their favorite email?
What fraction of Democrats?
Independents?
b.
Is there a
statistically significant difference between the fraction of Republicans using
AOL and the fraction of Democrats? What
is the p-value of this test?
c.
What is the most
popular email?
d.
What is the
probability that a person is a Republican, conditional on citing AOL as their
favorite email provider?
13.
A recent news item
reported this experiment. Survey
participants were asked, among various questions, whether they supported Tea
Party views. Later they were asked the
extent to which they blamed homeowners for getting themselves into debt
troubles (on a scale of 1 to 7 where 7 indicated a great deal of blame for the
individual). However there was a subtle
twist: some surveys showed a photo illustration of a white man in front of a
home but others showed a photo of a black man.
Of the tea party supporters, 107 viewed the question with a black man
illustrating; 101 viewed the question with a white man illustrating. Of the non-tea party supporters, 292 viewed
the version with a black man, 300 saw the white man. Of tea-party supporters who saw the black
man, the average blame rating was 4.72 with standard deviation of 2.23; of
tea-party supporters who saw the white man, the average blame was 4.16 with
standard deviation of 1.78. For non-tea
party supporters who saw the black guy, the average blame was 3.92 with
standard deviation of 1.87; for non-tea party supporters who saw the white guy
the average blame was 4.00 with standard deviation of 1.61. (The full results have not been released so
these represent my guesses about numbers of observations.)
a.
Explain if there
is a significant difference (form a hypothesis test, find test statistic and
p-value, make a conclusion). What can be
concluded from this survey?
b.
Suppose you
created an analogous survey for people who supported Occupy Wall Street
(OWS). What questions would you ask
them? Can you suggest a different twist
of how to mix visual cues, that could elicit interesting information?
14.
This question uses
the BRFSS data on InYourClass or Blackboard. One question asks people how satisfied they
are with their life, on a scale of 1 to 4 where 1 is "very satisfied"
and 4 is "very dissatisfied".
Looking at people between 25 and 35 years old, we divide the sample into
the 12,521 who do not have any college education and the 26889 who have either
some college or a 4-year degree or more.
The average satisfaction of people without any college education is 1.73
with a standard deviation of 0.646. The
average satisfaction of people with some college is 1.55 with a standard
deviation of 0.593.
a.
Form a hypothesis
test for whether the difference in life satisfaction is statistically
significant. What is the p-value? Explain how this affects our judgment of
whether college makes a person happy.
b.
Using the data
set, explore what other factors could account for the difference in life
satisfaction.
15.
Continuing with
the BRFSS data, look at other differences between people who went to college
and those who didn't go to college.
Different numbers of people answered these questions so note the number
of observations in each comparison. We
look at whether or not people exercised and whether they had ever smoked. We see that 68.82% of the 13,868 non-college
people exercised while 83.21% of the 28,501 college people exercised. Also 50.87% of 13,764 non-college had ever
smoked while, of the 28,370 respondents
who had been to college, just 33.11% had ever smoked.
a.
Form hypothesis
tests for differences in exercise and smoking.
Give p-values.
b.
Using the data,
explore the other factors that could explain these differences.
16.
I provide PUMS
data for people in NYC (download from Blackboard or InYourClass;
pums_NYC_3.zip) to examine people's choices about when to begin commuting. The variable "begin_commute_time"
gives the hour of the day (from 0, midnight, to 23.5, 11:30pm) at which people
report that they leave for work (those who do not work are coded as -9 for
missing).
a.
What fraction
leave for work before 8am? What are some
of the important factors that explain this difference?
b.
Estimate a linear
regression to explain the time that someone leaves for work – you can assume
this is a continuous variable. What
variables should be in this regression?
What variables are statistically significant? What do you learn from this regression? Have you omitted any important variables that
are not in the data set? Discuss.
c.
Repeat the linear
regression but only include people who leave before 9am. How does this change the estimated
coefficients? What do you learn from
this regression?
17.
You might sketch a
picture.
a.
For a Normal Distribution with mean 4 and standard
deviation of 1, what is the area to the left of 3.3? 0.484 0.758 0.242 0.363
b.
For a Normal Distribution with mean -13 and
standard deviation of 7, what is the area to the left of -3.2? 0.162 0.081 0.919 0.758
c.
For a Normal Distribution with mean 1 and standard
deviation of 4, what is the area to the right of -6.6? 0.829 0.029 0.971 0.057
d.
For a Normal Distribution with mean -6 and standard
deviation of 2, what is the area to the right of -9.8? 0.057 0.829 0.029 0.971
e.
For a Normal Distribution with mean -3 and standard
deviation of 5, what is the area to the right of -8? 0.691 0.317 0.841 0.159
f.
For a Normal Distribution with mean -12 and
standard deviation of 5, what is the area in both tails farther from the mean
(in absolute value) than -21.5? 0.057
0.029 0.971 0.351
g.
For a
Normal Distribution with mean -9 and standard deviation of 5, what is
the area in both tails farther from the mean (in absolute value) than -10? 0.579 0.421
0.841 0.087
h.
For a Normal Distribution with mean -13 and
standard deviation of 8 what value leaves 0.22 in the right tail? -3.188 -3.607 -8.303 -11.792
i.
For a Normal Distribution with mean -7 and standard
deviation of 5 what value leaves 0.24 in the right tail? -4.026 -6.749 -1.052 -1.125
j.
For a Normal Distribution with mean 12 and standard
deviation of 2 what value leaves 0.03 in the right tail? 15.110 16.340 13.024 14.048
18.
You might sketch a
picture.
a.
For a t Distribution with sample average of 1.43,
standard error of 1.22, and 11 observations, what is the area in both tails,
for a null hypothesis of zero mean? 0.133
0.181 0.412
0.266
b.
For a t Distribution with sample average of 2.9,
standard error of 1.82, and 13 observations, what is the area in both tails,
for a null hypothesis of zero mean?
0.068 0.541 0.012 0.135
c.
For a t Distribution with sample average of 3.31,
standard error of 2.16, and 9 observations, what is the area in both tails, for
a null hypothesis of zero mean? 0.009 0.160
0.530 0.080
d.
For a t Distribution with sample average of 1.47,
standard error of 1.47, and 16 observations, what is the area in both tails,
for a null hypothesis of zero mean? 0.332 0.166
0.332
0.161
e.
For a t Distribution with 20 observations and
standard error of 2.53, what sample mean leaves 0.08 in the two tails, when
testing a null hypothesis of zero? 0.922
1.844
3.689 4.666
f.
For a t Distribution with 5 observations and
standard error of 2.78, what sample mean leaves 0.2 in the two tails, when
testing a null hypothesis of zero? 0.738 1.476
4.103
2.952
g.
For a t Distribution with 20 observations and
standard error of 0.53, what sample mean leaves 0.24 in the two tails, when
testing a null hypothesis of zero? 1.211
0.606 0.642
2.422
h.
Sample A has mean
4.28, standard error of 0.21, and 4 observations. Sample B has mean 4.99, standard deviation of
0.33, and 23 observations. Test the null
hypothesis of no difference. 0.005
0.002
0.906 0.517
i.
Sample A has mean
1.6, standard error of 0.68, and 9 observations. Sample B has mean 4.83, standard deviation of
2.81, and 9 observations. Test the null
hypothesis of no difference. 0.360 0.009
0.010
0.004
19.
You are given the
following data on the number of people in the PUMS sample who live in each of
the five boroughs of NYC and who commute in each specified manner (where
'other' includes walking, working from home, taking a taxi or ferry or rail).
|
Bronx |
Manhattan |
Staten Is |
Brooklyn |
Queens |
|
|
car |
5788 |
2692 |
5526 |
10990 |
16905 |
|
bus |
3132 |
2789 |
1871 |
4731 |
4636 |
|
subway |
6481 |
13260 |
279 |
18951 |
14025 |
|
other |
2748 |
10327 |
900 |
6587 |
4877 |
a.
Find the Joint Probability
for drawing, from this sample, a person from Queens who commutes by bus. Find the Joint Probability of a person from
the Bronx who commutes by subway.
b.
Find the Marginal
Probability of drawing, from among the people who commute by subway, someone
who lives in Brooklyn. Find the Marginal
Probability, of people who commute by bus, someone who lives in the Bronx.
c.
Find the Marginal
Probability of drawing, from among the people who live in Staten Island,
someone who drives a car to work. Find
the Marginal Probability, of people in Brooklyn, who commute by subway.
d.
Are these two
choices (which borough to live in, how to commute) independent? Explain using the definition of statistical
independence.
20.
To investigate an
hypothesis proposed by a student, I got data, for 102 of the world's major
countries, on the fraction of the population who are religious as well as the
income per capita and the enrollment rate of boys and girls in primary
school. The hypothesis to be
investigated is whether more religious societies tend to hold back women. I ran two separate models: Model 1 uses girls
enrollment rate as the dependent; Model 2 uses the ratio of girls to boys enrollment rates as the dependent. The results are below (standard errors in
italics and parentheses below each coefficient):
|
Model
1 |
Model
2 |
t-stat |
p-value |
|
|
Intercept |
137 |
1.12 |
|
|
|
(18) |
(0.09) |
|
|
|
|
Religiosity |
-0.585 |
-0.0018 |
|
|
|
(0.189) |
(0.0009) |
|
|
|
|
GDP
per capita |
0.00056 |
0.0000016 |
|
|
|
(0.00015) |
(0.0000007) |
|
|
a.
Which coefficient
estimates are statistically significant?
What are the t-statistics and p-values for each?
b.
How would you
interpret these results?
c.
Critique the
regression model. How would you improve
it?
21.
Download the data,
"PUMA_nyc_for_exam" from Blackboard, which
gives PUMA data on people living in the 5 boroughs. Run a regression that models the variable,
"GRPIP," "Gross Rent as Percent of Income," which tells how
burdensome are housing costs for different people.
a.
What are the mean,
median, 25th, and 75th percentiles for Rent as a fraction
of income? Does this seem
reasonable?
b.
What is the
fraction spent on rent by households in Brooklyn? In Queens?
Is the difference statistically significant? Between Brooklyn and the Bronx?
c.
What variables
might be important in explaining this ratio? Find summary statistics for these
variables.
d.
Run a regression
and interpret the output. Which
variables are statistically significant?
How do you interpret their coefficients?
Are these reasonable?
e.
What variables are
omitted? How could the regression be
improved (using actual real data)? Can
you estimate a better model (with squared terms, interaction terms, etc)?
22.
A random variable
is distributed as a standard normal.
(You are encouraged to sketch the PDF in each case.)
a.
What is the
probability that we could observe a value as far or farther than 1.3?
b.
What is the
probability that we could observe a value nearer than 1.8?
c.
What value would
leave 10% of the probability in the right-hand tail?
d.
What value would
leave 25% in both the tails (together)?
23.
Using the CPS 2010
data (on Blackboard, although you don't need to download it for this),
restricting attention to only those reporting a non-zero wage and salary, the
following regression output is obtained for a regression (including industry,
occupation, and state fixed effects) with wage and salary as the dependent
variable.
a.
Fill in the missing values in the table.
b.
The dummy
variables for veterans have been split into various time periods to distinguish
recent veterans from those who served decades ago. If you knew that the draft ended at about the
same time as the Vietnam war, how would that affect your interpretation of the
coefficient estimates?
c.
Critique the
regression: how would you improve the estimates (using the same dataset)?
|
ANOVAb |
||||||
|
Model |
Sum of
Squares |
df |
Mean
Square |
F |
Sig. |
|
|
1 |
Regression |
8.201E+13 |
152 |
5.395E+11 |
324.098 |
.000a |
|
Residual |
1.639E+14 |
98479 |
1.665E+09 |
|
|
|
|
Total |
2.460E+14 |
98631 |
|
|
|
|
Coefficientsa |
|||||||
|
Model |
Unstandardized
Coefficients |
Standardized
Coefficients |
t |
Sig. |
|||
|
B |
Std.
Error |
Beta |
|||||
|
1 |
(Constant) |
12970.923 |
2290.740 |
|
5.662 |
.000 |
|
|
|
Demographics, Age |
2210.038 |
62.066 |
.605 |
____ |
____ |
|
|
|
Age squared |
-21.527 |
.693 |
-.504 |
____ |
____ |
|
|
|
Female |
-14892.950 |
____ |
-.149 |
-47.872 |
.000 |
|
|
|
African American |
-3488.065 |
____ |
-.022 |
-7.809 |
.000 |
|
|
|
Asian |
-2700.032 |
____ |
-.012 |
-2.782 |
.005 |
|
|
|
Native American Indian or Alaskan or Hawaiian |
____ |
824.886 |
-.009 |
-3.442 |
.001 |
|
|
|
Hispanic |
____ |
483.313 |
-.024 |
-6.847 |
.000 |
|
|
|
Immigrant |
____ |
632.573 |
-.032 |
-6.728 |
.000 |
|
|
|
1 or more parents were immigrants |
989.451 |
541.866 |
.008 |
____ |
____ |
|
|
|
immig_india |
-456.482 |
1675.840 |
-.001 |
____ |
____ |
|
|
|
immig_SEAsia |
821.730 |
1252.853 |
.003 |
____ |
____ |
|
|
|
immig_MidE |
-599.852 |
2335.868 |
-.001 |
____ |
____ |
|
|
|
immig_China |
3425.017 |
1821.204 |
.006 |
____ |
____ |
|
|
|
Education: High School Diploma |
2786.569 |
492.533 |
.025 |
5.658 |
.000 |
|
|
|
Education: Some College but no degree |
5243.544 |
528.563 |
.042 |
9.920 |
.000 |
|
|
|
Education: Associate in vocational |
6530.542 |
762.525 |
.028 |
8.564 |
.000 |
|
|
|
Education: Associate in academic |
7205.474 |
736.838 |
.032 |
9.779 |
.000 |
|
|
|
Education: 4-yr degree |
17766.941 |
576.905 |
.143 |
30.797 |
.000 |
|
|
|
Education: Advanced Degree |
36755.485 |
703.658 |
.227 |
52.235 |
.000 |
|
|
|
Married |
4203.602 |
414.288 |
.042 |
10.147 |
.000 |
|
|
|
Divorced or Widowed or Separated |
830.032 |
501.026 |
.006 |
1.657 |
.098 |
|
|
|
kids_under18 |
3562.643 |
327.103 |
.036 |
10.891 |
.000 |
|
|
|
kids_under6 |
-721.123 |
404.818 |
-.006 |
-1.781 |
.075 |
|
|
|
Union member |
4868.240 |
976.338 |
.013 |
4.986 |
.000 |
|
|
|
Veteran since Sept 2001 |
2081.909 |
4336.647 |
.001 |
.480 |
.631 |
|
|
|
Veteran Aug 1990 - Aug 2001 |
-1200.688 |
1788.034 |
-.002 |
-.672 |
.502 |
|
|
|
Veteran May 1975-July 1990 |
-1078.953 |
1895.197 |
-.001 |
-.569 |
.569 |
|
|
|
Veteran August 1964-April 1975 |
-6377.461 |
3195.784 |
-.005 |
-1.996 |
.046 |
|
|
|
Veteran Feb 1955-July 1964 |
-7836.420 |
4904.511 |
-.004 |
-1.598 |
.110 |
|
|
|
Veteran July 1950-Jan 1955 |
-19976.382 |
10570.869 |
-.005 |
-1.890 |
.059 |
|
|
|
Veteran before 1950 |
-15822.026 |
12943.766 |
-.003 |
-1.222 |
.222 |
|
24.
Using the NHANES 2007-09 data (on Blackboard,
although you only need to download it for the very last part), reporting a
variety of socioeconomic variables as well as behavior choices such as the
number of sexual partners reported (number_partners),
we want to see if richer people have more sex than poor people. The following table is constructed, showing
three categories of family income and 5 categories of number of sex partners:
|
number of sex partners |
||||||
|
family income |
zero |
1 |
2 - 5 |
6 - 25 |
>25 |
Marginal: |
|
< 20,000 |
11 |
63 |
236 |
255 |
92 |
______ |
|
20 - 45,000 |
7 |
117 |
323 |
308 |
117 |
______ |
|
> 45,000 |
3 |
234 |
517 |
607 |
218 |
______ |
|
Marginal: |
______ |
______ |
______ |
______ |
______ |
|
a.
Where is the
median, for number of sex partners, for poorer people? For middle-income people? For richer people?
b.
Conditional on a
person being poorer, what is the likelihood that they report fewer than 6
partners? Conditional on being
middle-income? Richer?
c.
Conditional on
reporting 2-5 sex partners, what is the likelihood that a person is
poorer? Middle-income? Richer?
d.
Explain why the
average number of sex partners might not be as useful a measure as, for
example, the data ranges above or the median or the 95%-trimmed mean.
e.
(5 points) (You
will need to download the data for this part) Could the difference be explained
by schooling effects? How does college
affect the number of sex partners?
25.
I provide a
dataset online (stock_indexes.sav on InYourClass)
with the S&P 500 stock index and its daily returns as well as the NASDAQ
index and its returns, from January 1, 1980 to December 9, 2010.
a.
What is the mean
and standard deviation?
b.
If the stock index
returns were distributed normally, what value of return is low enough, that 95%
of the days are better?
c.
What is the 5%
value of the actual returns (the fifth percentile, use
"Analyze\Descriptive Statistics\Explore" and check
"Percentiles" in "Options")? Is this different from your previous
answer? What does that imply? Explain.
26.
Using the CPS 2010 data online, examine
whether children are covered by Medicaid or other insurance plan. Run a crosstab on "CH_HI" whether a
child has health insurance, and "CH_MC" if a child is covered by
Medicaid.
a.
What fraction of
children are covered by Medicaid? What
fraction of children are not covered by any policy?
b.
What is the
average family income of children who are covered by Medicaid? Of children who are not? What is the t-statistic and p-value for a
statistical test of whether the means are equal?
27.
The oil and gas
price dataset online, (oil_gas_prices.sav on InYourClass,
although you only need to download it for the very last part), has data on
prices of oil, gasoline, and heating oil (futures prices, in this case). Compare two regression specifications of the
current price of gasoline. Specification
A explains the current price with its price the day before. Specification B has the price of gas on the
day before but also includes the prices of crude oil and heating oil on the day
before. The estimates of the coefficient
on gasoline are shown below:
|
|
Coefficient estimate |
Standard error |
|
Specification A |
0.021 |
0.028 |
|
Specification B |
0.153 |
0.048 |
a.
Calculate
t-statistics and p-values for each specification of the regression.
b.
Explain what you
could learn from each of these regressions – specifically, would it be a good
idea to invest in gasoline futures?
c.
Explain why there
is a difference in the estimated coefficients.
Can you say that one is more correct?
28.
A random variable
is distributed as a standard normal.
(You are encouraged to sketch the PDF in each case.)
d.
What is the
probability that we could observe a value as far or farther than -0.9?
e.
What is the
probability that we could observe a value nearer than 1.4?
f.
What value would
leave 5% of the probability in the right-hand tail?
g.
What value would
leave 5% in both the tails (together)?
29.
[this question was
given in advance for students to prepare with their group} Download (from
Blackboard) and prepare the dataset on the 2004 Survey of Consumer Finances
from the Federal Reserve. Estimate the
probability that each head of household (restrict to only heads of household!)
has at least one credit card. Write up a
report that explains your results (you might compare different specifications,
you might consider different sets of socioeconomic variables, different
interactions, different polynomials, different sets of fixed effects, etc.).
30.
Explain in greater
detail your topic for the final project.
Include details about the dataset which you will use and the regressions
that you will estimate. Cite at least
one previous study which has been done on that topic (published in a refereed
journal).
31.
You want to
examine the impact of higher crude oil prices on American driving habits during
the past oil price spike. A regression
of US gasoline purchases on the price of crude oil as well as oil futures gives
the coefficients below. Critique the
regression and explain whether the necessary basic assumptions hold. Interpret each coefficient; explain its
meaning and significance.
Coefficients(a)
|
Model |
|
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
|
| B |
Std. Error |
Beta |
||||
|
1 |
(Constant) |
.252 |
.167 |
|
1.507 |
.134 |
| return on
crude futures, 1 month ahead |
.961 |
.099 |
.961 |
9.706 |
.000 |
|
| return on
crude futures, 2 months ahead |
-.172 |
.369 |
-.159 |
-.466 |
.642 |
|
| return on
crude futures, 3 months ahead |
.578 |
.668 |
.509 |
.864 |
.389 |
|
| return on
crude futures, 4 months ahead |
-.397 |
.403 |
-.333 |
-.986 |
.326 |
|
| US gasoline
consumption |
-.178 |
.117 |
-.036 |
-1.515 |
.132 |
|
| Spot Price
Crude Oil Cushing, OK WTI FOB (Dollars per Barrel) |
4.23E-005 |
.000 |
.042 |
1.771 |
.079 |
|
a Dependent Variable:
return on crude spot price
32.
You estimate the
following coefficients for a regression explaining log individual incomes:
Coefficients(a)
|
Model |
|
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
|
| B |
Std. Error |
Beta |
B |
Std. Error |
||
|
1 |
(Constant) |
6.197 |
.026 |
|
239.273 |
.000 |
| Demographics,
Age |
.154 |
.001 |
1.769 |
114.120 |
.000 |
|
| agesq |
-.002 |
.000 |
-1.594 |
-107.860 |
.000 |
|
| female |
-.438 |
.017 |
-.184 |
-25.670 |
.000 |
|
| afam |
-.006 |
.010 |
-.002 |
-.590 |
.555 |
|
| asian |
-.011 |
.015 |
-.002 |
-.713 |
.476 |
|
| Amindian |
-.063 |
.018 |
-.009 |
-3.573 |
.000 |
|
| Hispanic |
.053 |
.010 |
.016 |
5.139 |
.000 |
|
| ed_hs |
.597 |
.014 |
.226 |
43.251 |
.000 |
|
| ed_smcol |
.710 |
.014 |
.272 |
50.150 |
.000 |
|
| ed_coll |
1.138 |
.015 |
.379 |
74.378 |
.000 |
|
| ed_adv |
1.388 |
.018 |
.355 |
78.917 |
.000 |
|
| Married |
.222 |
.009 |
.092 |
25.579 |
.000 |
|
| Divorced
Widowed Separated |
.138 |
.011 |
.041 |
12.311 |
.000 |
|
| union |
.189 |
.021 |
.022 |
8.951 |
.000 |
|
| veteran |
.020 |
.012 |
.004 |
1.646 |
.100 |
|
| immigrant |
-.055 |
.013 |
-.017 |
-4.116 |
.000 |
|
| 2nd
Generation Immigrant |
.064 |
.012 |
.022 |
5.268 |
.000 |
|
| female*ed_hs |
-.060 |
.020 |
-.017 |
-2.948 |
.003 |
|
| female*ed_smcol |
-.005 |
.020 |
-.002 |
-.270 |
.787 |
|
| female*ed_coll |
-.104 |
.022 |
-.026 |
-4.806 |
.000 |
|
| female*ed_adv |
-.056 |
.025 |
-.010 |
-2.218 |
.027 |
|
a Dependent Variable: lnwage
a.
Explain your
interpretation of the final four coefficients in the table.
b.
How would you test
their significance? If this test got
"Sig. = 0.13" from SPSS, interpret the result.
c.
What variables are
missing? Explain how this might affect
the analysis.
33.
Fill in the blanks
in the following table showing SPSS regression output. The model has the dependent variable as time
spent working at main job.
Coefficients(a)
|
Model |
|
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
|
| B |
Std. Error |
Beta |
||||
|
1 |
(Constant) |
198.987 |
7.556 |
|
26.336 |
.000 |
| female |
-65.559 |
4.031 |
-.138 |
___?___ |
___?___ |
|
| African-American |
-9.190 |
6.190 |
-.013 |
___?___ |
___?___ |
|
| Hispanic |
17.283 |
6.387 |
.024 |
___?___ |
___?___ |
|
| Asian |
1.157 |
12.137 |
.001 |
___?___ |
___?___ |
|
| Native
American/Alaskan Native |
-28.354 |
14.018 |
-.017 |
-2.023 |
.043 |
|
| Education:
High School Diploma |
___?___ |
6.296 |
.140 |
11.706 |
.000 |
|
| Education:
Some College |
___?___ |
6.308 |
.174 |
14.651 |
.000 |
|
| Education:
4-year College Degree |
110.064 |
___?___ |
.183 |
16.015 |
.000 |
|
| Education:
Advanced degree |
126.543 |
___?___ |
.166 |
15.714 |
.000 |
|
| Age |
-1.907 |
___?___ |
-.142 |
-16.428 |
.000 |
|
a Dependent Variable: Time Working at main job
34.
Suppose I were to
start a hedge fund, called KevinNeedsMoney Limited
Ventures, and I want to present evidence about how my fund did in the
past. I have data on my fund's returns, Rett, at each time period t, and the returns on the market,
Mktt. The
graph below shows the relationship of these two variables:
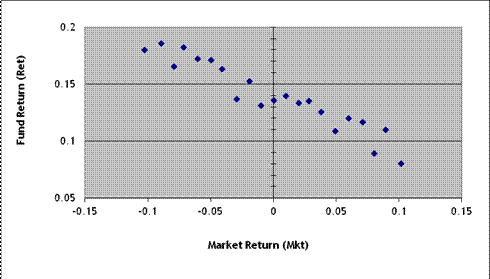
a.
I run a univariate OLS regression, ![]() . Approximately what value would be estimated for the
intercept term, b0? For the slope term, b1?
. Approximately what value would be estimated for the
intercept term, b0? For the slope term, b1?
b.
How would you
describe this fund's performance, in non-technical language – for instance if
you were advising a retail investor without much finance background?
35.
Using the American
Time Use Study (ATUS) we measure the amount of time that each person reported
that they slept. We run a regression to
attempt to determine the important factors, particularly to understand whether
richer people sleep more (is sleep a normal or inferior good) and how sleep is
affected by labor force participation.
The SPSS output is below.
|
Coefficients(a) |
|
|
|
|
|
||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
|
|
|||
|
|
|
B |
Std. Error |
Beta |
t |
Sig. |
|
|
1 |
(Constant) |
-4.0717 |
4.6121 |
|
-0.883 |
0.377 |
|
|
|
female |
23.6886 |
1.1551 |
0.18233 |
20.508 |
0.000 |
|
|
|
African-American |
-8.5701 |
1.7136 |
-0.04369 |
-5.001 |
0.000 |
|
|
|
Hispanic |
10.1015 |
1.7763 |
0.05132 |
5.687 |
0.000 |
|
|
|
Asian |
-1.9768 |
3.3509 |
-0.00510 |
-0.590 |
0.555 |
|
|
|
Native
American/Alaskan Native |
-3.5777 |
3.8695 |
-0.00792 |
-0.925 |
0.355 |
|
|
|
Education:
High School Diploma |
2.5587 |
1.8529 |
0.01768 |
1.381 |
0.167 |
|
|
|
Education:
Some College |
-0.3234 |
1.8760 |
-0.00222 |
-0.172 |
0.863 |
|
|
|
Education:
4-year College Degree |
-1.3564 |
2.0997 |
-0.00821 |
-0.646 |
0.518 |
|
|
|
Education:
Advanced degree |
-3.3303 |
2.4595 |
-0.01590 |
-1.354 |
0.176 |
|
|
|
Weekly
Earnings |
0.000003 |
0.000012 |
-0.00277 |
-0.246 |
0.806 |
|
|
|
Number
of children under 18 |
2.0776 |
0.5317 |
0.03803 |
3.907 |
0.000 |
|
|
|
person
is in the labor force |
-11.6706 |
1.7120 |
-0.08401 |
-6.817 |
0.000 |
|
|
|
has
multiple jobs |
0.4750 |
2.2325 |
0.00185 |
0.213 |
0.832 |
|
|
|
works
part time |
4.2267 |
1.8135 |
0.02244 |
2.331 |
0.020 |
|
|
|
in
school |
-5.4641 |
2.2993 |
-0.02509 |
-2.376 |
0.017 |
|
|
|
Age |
1.1549 |
0.1974 |
0.31468 |
5.850 |
0.000 |
|
|
|
Age-squared |
-0.0123 |
0.0020 |
-0.33073 |
-6.181 |
0.000 |
|
a.
Which variables
are statistically significant at the 5% level?
At the 1% level?
b.
How much more or
less time (in minutes) would be spent sleeping by a male college graduate who
is African-American and working full-time, bringing weekly earnings of $1000?
c.
Are there other
variables that you think are important and should be included in the
regression? What are they, and why?
36.
You are given the
following output from a logit regression using ATUS
data. The dependent variable is whether
the person spent any time cleaning in the kitchen and the independent variables
are the usual list of race/ethnicity (African-American, Asian, Native American,
Hispanic), female, educational attainment (high school diploma, some college, a
4-year degree, or an advanced degree), weekly earnings, the number of kids in
the household, dummies if the person is in the labor force, has multiple jobs,
works part-time, or is in school now, as well as age and age-squared. We include a dummy if there is a spouse or
partner present and then an interaction term for if the person is male AND
there is a spouse in the household.
There are only adults in the sample.
Descriptive statistics show that approximately 5% of men clean in the
kitchen while 20% of women do. The SPSS
output for the logit regression is:
|
|
B |
S.E. |
Wald |
df |
Sig. |
Exp(B) |
|
female |
0.9458 |
0.0860 |
120.945 |
1 |
0.000 |
2.5749 |
|
African-American |
-0.6113 |
0.0789 |
60.079 |
1 |
0.000 |
0.5427 |
|
Hispanic |
-0.2286 |
0.0765 |
8.926 |
1 |
0.003 |
0.7956 |
|
Asian |
0.0053 |
0.1360 |
0.001 |
1 |
0.969 |
1.0053 |
|
Native
American |
-0.0940 |
0.1618 |
0.338 |
1 |
0.561 |
0.9103 |
|
Education:
high school |
0.0082 |
0.0789 |
0.011 |
1 |
0.917 |
1.0082 |
|
Education:
some college |
0.0057 |
0.0813 |
0.005 |
1 |
0.944 |
1.0057 |
|
Education:
college degree |
0.0893 |
0.0887 |
1.013 |
1 |
0.314 |
1.0934 |
|
Education:
advanced degree |
0.0874 |
0.1009 |
0.751 |
1 |
0.386 |
1.0914 |
|
Weekly
Earnings |
0.0000007 |
0.0000005 |
1.943 |
1 |
0.163 |
1.0000 |
|
Num.
Kids in Household |
0.2586 |
0.0226 |
131.473 |
1 |
0.000 |
1.2952 |
|
person
in the labor force |
-0.5194 |
0.0694 |
55.967 |
1 |
0.000 |
0.5949 |
|
works
multiple jobs |
-0.2307 |
0.1009 |
5.223 |
1 |
0.022 |
0.7940 |
|
works
part-time |
0.1814 |
0.0733 |
6.130 |
1 |
0.013 |
1.1989 |
|
person
is in school |
-0.1842 |
0.1130 |
2.658 |
1 |
0.103 |
0.8318 |
|
Age |
0.0551 |
0.0088 |
38.893 |
1 |
0.000 |
1.0567 |
|
Age-squared |
-0.0004 |
0.0001 |
22.107 |
1 |
0.000 |
0.9996 |
|
spouse
is present |
0.5027 |
0.0569 |
78.074 |
1 |
0.000 |
1.6531 |
|
Male
* spouse is present |
-0.6562 |
0.1087 |
36.462 |
1 |
0.000 |
0.5188 |
|
Constant |
-3.3772 |
0.2317 |
212.434 |
1 |
0.000 |
0.0341 |
a.
Which variables
from the logit are statistically significant at the
5% level? At the 1% level?
b.
How would you
interpret the coefficient on the Male * spouse-present interaction term? What is the age when a person hits the peak
probability of cleaning?
37.
Use the SPSS
dataset, atus_tv from Blackboard, which is a subset
of the American Time Use survey. This
time we want to find out which factors are important in explaining whether
people spend time watching TV. There are
a wide number of possible factors that influence this choice.
a.
What fraction of
the sample spend any time watching TV?
Can you find sub-groups that are significantly different?
b.
Estimate a
regression model that incorporates the important factors that influence TV
viewing. Incorporate at least one
non-linear or interaction term. Show the
SPSS output. Explain which variables are
significant (if any). Give a short
explanation of the important results.
38.
This question
refers to your final project.
d.
What data set will
you use?
e.
What regression
(or regressions) will you run? Explain
carefully whether the dependent variable is continuous or a dummy, and what
this means for the regression specification.
What independent variables will you include? Will you use nonlinear specifications of any
of these? Would you expect heteroskedasticity?
f.
What other
variables are important, but are not measured and available in your data
set? How do these affect your analysis?
39.
Estimate the
following regression:: S&P100 returns = b0 + b1(lag S&P100 returns) + b2(lag interest rates) + ε
using the
dataset, financials.sav. Explain which
coefficients (if any) are significant and interpret them.
40.
A study by Mehran
and Tracy examined the relationship between stock option grants and measures of
the company's performance. They
estimated the following specification:
Options = b0+b1(Return on Assets)+b2(Employment)+b3(Assets)+b4(Loss)+u
where the
variable (Loss) is a dummy variable for whether the firm had negative
profits. They estimated the following
coefficients:
|
|
Coefficient |
Standard Error |
|
Return on Assets |
-34.4 |
4.7 |
|
Employment |
3.3 |
15.5 |
|
Assets |
343.1 |
221.8 |
|
Loss Dummy |
24.2 |
5.0 |
Which
estimate has the highest t-statistic (in absolute value)? Which has the lowest p-value? Show your calculations. How would you explain the estimate on the "Loss"
dummy variable?
41.
A paper by Farber
examined the choices of how many hours a taxidriver
would work, depending on a number of variables.
His output is:
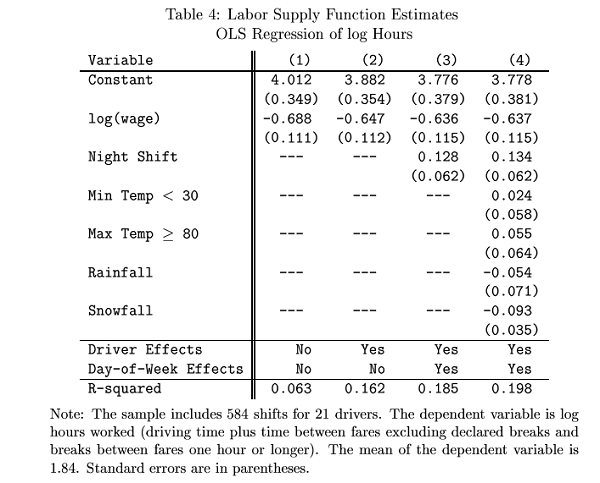
"Driver
Effects" are fixed effects for the 21 different drivers.
a.
What is the
estimated elasticity of hours with respect to the wage?
b.
Is there a
significant change in hours on rainy days?
On snowy days?
42.
A paper by Gruber
looks at the effects of divorce on children (once they become adults),
including whether there was an increase or decrease in education and
wages. Gruber uses data on state divorce
laws: over time some states changed their laws to make divorce easier (no-fault
or unilateral divorce). Why do you think
that he used state-level laws rather than the individual information (which was
in the dataset) about whether a person's parents were divorced? Is it important that he documents that states
with easier divorce laws had more divorces?
If he ran a regression that explained an adult's wage on the usual
variables, plus a measure of whether that person's parents had been divorced,
what complications might arise? Explain.
43.
Using the data on
New Yorkers in 1910, we estimate a binary logistic (logit)
model to explain labor force participation (whether each person was working for
pay) as a function of gender (a dummy variable for female), race (a dummy for
African-American), nativity (a dummy if the person is an immigrant and then
another dummy if they are second-generation – their parents were immigrants),
marital status (three dummies: one for married; one for Divorced/Separated; one
for Widow(er)s), age, age-squared, and interaction
effects. We allow interactions between
Female and Married (fem_marr = Married * Female), and
then between Age and Immigrant (age_immig = Age *
Immigrant) and Age-Squared and Immigrant (agesq_immig
= Age2 * Immigrant). Explain the following regression results:
Variables
in the Equation
|
|
B |
S.E. |
Wald |
df |
Sig. |
Exp(B) |
|
|
Step 1(a) |
female |
-1.890 |
.122 |
240.805 |
1 |
.000 |
.151 |
| AfricanAmer |
2.703 |
.235 |
132.625 |
1 |
.000 |
14.919 |
|
| Married |
1.144 |
.193 |
35.245 |
1 |
.000 |
3.141 |
|
| fem_marr |
-4.946 |
.209 |
562.000 |
1 |
.000 |
.007 |
|
| DivSep |
.251 |
.568 |
.195 |
1 |
.658 |
1.285 |
|
| Widow |
-1.238 |
.131 |
89.790 |
1 |
.000 |
.290 |
|
| immigrant |
1.575 |
1.167 |
1.822 |
1 |
.177 |
4.831 |
|
| immig2g |
.068 |
.117 |
.338 |
1 |
.561 |
1.070 |
|
| Age |
.114 |
.047 |
5.858 |
1 |
.016 |
1.121 |
|
| age_sqr |
-.00176 |
.001 |
7.137 |
1 |
.008 |
.998 |
|
| age_immig |
-.035 |
.068 |
.263 |
1 |
.608 |
.966 |
|
| agesq_immig |
0.00027 |
.001 |
.080 |
1 |
.777 |
1.000 |
|
| Constant |
1.069 |
.795 |
1.809 |
1 |
.179 |
2.911 |
|
a Variable(s) entered on step 1: female, AfricanAmer, Married, fem_marr, DivSep, Widow, immigrant, immig2g, age, age_sqr,
age_immig, agesq_immig.
At
what age do natives peak in their labor force participation? Immigrants?
Which is higher? The regression
shows that women are less likely to be in the labor force, married people are
more likely, African-Americans are more likely, and immigrants are more likely
to be in the labor force. Interpret the
coefficient on the female-married interaction.
44.
Calculate the
probability in the following areas under the Normal pdf
with mean and standard deviation as given.
You might usefully draw pictures as well as making the
calculations. For the calculations you
can use either a computer or a table.
a.
What is the
probability, if the true distribution has mean -15 and standard deviation of
9.7, of seeing a deviation as large (in absolute value) as -1?
b.
What is the
probability, if the true distribution has mean 0.35 and standard deviation of
0.16, of seeing a deviation as large (in absolute value) as 0.51?
c.
What is the
probability, if the true distribution has mean -0.1 and standard deviation of
0.04, of seeing a deviation as large (in absolute value) as -0.16?
45.
Using data from
the NHIS, we find the fraction of children who are female, who are Hispanic,
and who are African-American, for two separate groups: those with and those
without health insurance. Compute tests
of whether the differences in the means are significant; explain what the tests
tell us. (Note that the numbers in
parentheses are the standard deviations.)
|
|
with health insurance |
without health insurance |
|
female |
0.4905 (0.49994) N=7865 |
0.4811 (0.49990) N=950 |
|
Hispanic |
0.2587 (0.43797) N=7865 |
0.5411 (0.49857) N=950 |
|
African American |
0.1785 (0.38297) N=7865 |
0.1516 (0.35880) N=950 |
46.
Explain the topic
of your final project. Carefully explain
one regression that you are going to estimate (or have already estimated). Tell the dependent variable and list the
independent variables. What hypothesis
tests are you particularly interested in?
What problems might arise in the estimation? Is there likely to be heteroskedasticity? Is it clear that the X-variables cause the
Y-variable and not vice versa?
Explain. [Note: these answers
should be given in the form of well-written paragraphs not a series of bullet
items answering my questions!]
47.
In estimating how
much choice of college major affects income, Hamermesh
& Donald (2008) send out surveys to college alumni. They first estimate the probability that a
person will answer the survey with a probit
model. They use data on major (school of
education is the omitted category), how long ago the person graduated, and some
information from their college record.
Their results are (assume that the 0 coefficient is 0.253):
|
|
|
pr(respond to survey) |
t-statistic |
|
Major (Dummy variable) |
Architecture and
Fine Arts |
-0.044 |
1.61 |
|
Business---general
|
0.046 |
1.72 |
|
|
Business---quantitative |
0.038 |
1.45 |
|
|
Communications |
0.023 |
1.00 |
|
|
Engineering |
0.086 |
2.51 |
|
|
Humanities |
-0.013 |
0.54 |
|
|
"Honors" |
0.087 |
2.08 |
|
|
Social Sciences |
0.052 |
2.28 |
|
|
Natural Sciences,
Pharmacology |
0.04 |
1.52 |
|
|
Nursing, Social
Work |
0.061 |
1.57 |
|
|
dummy variables |
Class of 1980 |
0.025 |
1.61 |
|
Class of 1985 |
-0.009 |
0.61 |
|
|
Class of 1990 |
0.041 |
2.65 |
|
|
Class of 1995 |
0.033 |
2.20 |
|
|
|
GPA |
0.027 |
2.59 |
|
|
Upper Div. Sci.
& Math Credits |
0.0001 |
0.21 |
|
|
Upper Div. Sci.
& Math Grades |
0.002 |
0.51 |
|
|
HS Area Income
($000) |
0.001 |
1.92 |
|
|
Female |
0.031 |
3.06 |
What
is the probability of reply for a major in quantitative Business, from the
Class of 1995, with a GPA of 3.1, with 31 upper-division Science & Math
credits, with a 2.9 GPA within those upper-division Science & Math courses,
from a high school with a 40 HS Area Income?
How much more or less is the probability, if the respondent is female?
48.
Consider the
following regression output, from a regression of log-earnings on a variety of
socioeconomic factors. Fill in the
blanks in the "Coefficients" table.
Then calculate the predicted change in the dependent variable when Age
increases from 25 to 26; then when Age changes from 55 to 56 (note that
Age_exp2 is Age2 and Age_exp3 is Age3).
Model
Summary
|
Model |
R |
R Square |
Adjusted R Square |
Std. Error of the Estimate |
|
1 |
.613 |
.376 |
.376 |
.94098 |
ANOVA
|
Model |
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
1 |
Regression |
53551.873 |
26 |
2059.687 |
2326.152 |
.000(a) |
| Residual |
88995.531 |
100509 |
.885 |
|
|
|
| Total |
142547.403 |
100535 |
|
|
|
Coefficients(a)
|
Model |
|
Unstandardized
Coefficients |
Standardized Coefficients |
t |
Sig. |
|
|
|
|
|
B |
Std. Error |
Beta |
|
||
|
|
(Constant) |
3.841 |
0.059 |
|
65.581 |
0.000 |
|
|
|
Education: High School Diploma |
0.106 |
0.008 |
0.040305 |
__?__ |
__?__ |
ß |
|
|
Education: AS vocational |
__?__ |
0.015 |
0.051999 |
19.644 |
0.000 |
ß |
|
|
Education: AS academic |
0.344 |
__?__ |
0.062527 |
23.574 |
0.000 |
ß |
|
|
Education: 4 year College
Degree |
0.587 |
0.009 |
0.195326 |
65.257 |
0.000 |
|
|
|
Education: Advanced Degree |
0.865 |
0.011 |
0.221309 |
77.658 |
0.000 |
|
|
|
geog2 |
0.070 |
0.013 |
0.017072 |
5.220 |
0.000 |
|
|
|
geog3 |
0.005 |
0.013 |
0.001232 |
__?__ |
__?__ |
ß |
|
|
geog4 |
-0.050 |
0.013 |
-0.01345 |
__?__ |
__?__ |
ß |
|
|
geog5 |
0.062 |
0.012 |
0.019974 |
__?__ |
__?__ |
ß |
|
|
geog6 |
-0.061 |
0.017 |
-0.01039 |
__?__ |
__?__ |
ß |
|
|
geog7 |
0.026 |
0.014 |
0.006106 |
__?__ |
__?__ |
ß |
|
|
geog8 |
0.056 |
0.013 |
0.014445 |
4.303 |
0.000 |
|
|
|
geog9 |
0.102 |
0.012 |
0.030892 |
8.357 |
0.000 |
|
|
|
Married |
__?__ |
0.009 |
0.062911 |
17.213 |
0.000 |
ß |
|
|
Widowed |
__?__ |
0.025 |
-0.00191 |
-0.697 |
__?__ |
ß |
|
|
Divorced or Separated |
__?__ |
0.012 |
0.022796 |
7.042 |
0.000 |
ß |
|
|
female |
__?__ |
0.006 |
-0.19408 |
-76.899 |
0.000 |
ß |
|
|
union |
0.208 |
__?__ |
0.024531 |
9.808 |
0.000 |
ß |
|
|
hispanic |
-0.106 |
__?__ |
-0.03211 |
-12.012 |
0.000 |
ß |
|
|
Af_Amer |
-0.038 |
__?__ |
-0.00995 |
-3.774 |
0.000 |
ß |
|
|
NativAm |
-0.100 |
__?__ |
-0.01342 |
-5.322 |
0.000 |
ß |
|
|
AsianAm |
-0.061 |
__?__ |
-0.01147 |
-4.420 |
0.000 |
ß |
|
|
MultRace |
0.001 |
0.066 |
1.93E-05 |
0.008 |
__?__ |
ß |
|
|
Demographics, Age |
0.377 |
0.005 |
4.332516 |
83.265 |
0.000 |
|
|
|
Age_exp2 |
-0.00689 |
0.00011 |
-6.70717 |
-65.345 |
0.000 |
|
|
|
Age_exp3 |
0.0000384 |
0.0000008 |
2.65889 |
49.301 |
0.000 |
|
a Dependent Variable: ln_earn
49.
Use the dataset
brfss_exam2.sav. This has data from the
Behavioral Risk Factors Survey, focused on people under 30 years old. Carefully estimate a model to explain the
likelihood that a person has smoked (measured by variable "eversmok").
Note that I have created some basic dummy variables but you are
encouraged to create more of your own, as appropriate. Explain the results of your model in
detail. Are there surprising coefficient
estimates? What variables have you left
out (perhaps that aren't in this dataset but could have been collected), that
might be important? How is this omission
likely to affect the estimated model?
What is the change in probability of smoking, between a male and female
(explain any other assumptions that you make, to calculate this)?
50.
Using the CPS 2010
data (you don't need to download it for this), restricting attention to only
prime-age (25-55 year-old) males reporting a non-zero wage and salary, the
following regression output is obtained for a regression (including industry,
occupation, and state fixed effects) with log wage and salary as the dependent
variable.
a.
(17 points) Fill
in the missing values in the table.
b.
(3 points)
Critique the regression: how would you improve the estimates (using the same
dataset)?
|
Model |
Sum of
Squares |
df |
Mean
Square |
F |
Sig. |
|
|
1 |
Regression |
11194.359 |
145 |
77.202 |
127.556 |
.000a |
|
Residual |
21558.122 |
35619 |
.605 |
|
|
|
|
Total |
32752.482 |
35764 |
|
|
|
|
|
Coefficientsa |
||||||
|
Model |
Unstandardized
Coefficients |
Standardized
Coefficients |
t |
Sig. |
||
|
B |
Std.
Error |
Beta |
||||
|
1 |
(Constant) |
8.375 |
.112 |
|
74.714 |
.000 |
|
|
Demographics, Age |
.078 |
.005 |
.705 |
|
|
|
|
Age squared |
-.00085 |
.00006 |
-.617 |
|
|
|
|
African American |
-.184 |
.015 |
-.058 |
|
|
|
|
Asian |
|
.022 |
-.025 |
-4.620 |
.000 |
|
|
Native American Indian or Alaskan or Hawaiian |
|
.027 |
-.025 |
-5.674 |
.000 |
|
|
Hispanic |
-.051 |
|
-.020 |
-2.172 |
.030 |
|
|
Mexican |
-.021 |
|
-.007 |
-.868 |
.386 |
|
|
Puerto Rican |
.014 |
|
.002 |
.319 |
.750 |
|
|
Cuban |
.007 |
.059 |
.001 |
|
|
|
|
Immigrant |
-.094 |
.019 |
-.039 |
|
|
|
|
1 or more parents were immigrants |
.001 |
.018 |
.001 |
|
|
|
|
Education: High School Diploma |
.219 |
|
.105 |
13.582 |
.000 |
|
|
Education: Some College but no degree |
.333 |
|
.130 |
18.332 |
.000 |
|
|
Education: Associate in vocational |
.362 |
|
.081 |
14.919 |
.000 |
|
|
Education: Associate in academic |
|
.025 |
.080 |
14.642 |
.000 |
|
|
Education: 4-yr degree |
|
.019 |
.236 |
28.773 |
.000 |
|
|
Education: Advanced Degree |
|
.023 |
.253 |
33.757 |
.000 |
|
|
Married |
|
.011 |
.140 |
25.219 |
.000 |
|
|
Divorced or Widowed or Separated |
|
.016 |
.021 |
3.992 |
.000 |
|
|
Union member |
|
.030 |
.031 |
7.168 |
.000 |
|
|
Veteran since Sept 2001 |
-.047 |
.094 |
-.002 |
|
|
|
|
Veteran Aug 1990 - Aug 2001 |
-.053 |
.038 |
-.006 |
|
|
|
|
Veteran May 1975-July 1990 |
.035 |
.048 |
.003 |
|
|
|
|
Veteran August 1964-April 1975 |
.078 |
.129 |
.003 |
|
|
51.
Using the BRFSS 2009 data, the following table
compares the reported health status of the respondent with whether or not they
smoked (defined as having at least 100 cigarettes)
|
SMOKED AT
LEAST 100 CIGARETTES |
||||
|
Yes |
No |
Marginal |
||
|
GENERAL HEALTH |
Excellent |
27775 |
49199 |
____ |
|
Very good |
58629 |
77357 |
____ |
|
|
Good |
64237 |
67489 |
____ |
|
|
Fair |
31979 |
26069 |
____ |
|
|
Poor |
15680 |
9191 |
____ |
|
|
Marginal |
____ |
____ |
||
a.
What is the median
health status for those who smoked? For
non-smokers?
b.
Fill in the
marginal probabilities – make sure they are probabilities.
c.
Explain what you
might conclude from this data.
52.
Using the CPS
data, run at least 4 interesting regressions to model the wages earned. Carefully explain what we can learn from each
regression: does it accord with theory; if not, what does this mean? Explain what statistical measures allow us to
compare different specifications.
53.
For a Normal
Distribution with mean 9 and standard
deviation 9.1, what is area to the right of -8.3?
A. 0.8387 B.
0.9713 C. 0.1587 D. 0.0287
54.
For a Normal
Distribution with mean 1 and standard
deviation 9.6, what is area to the right of 23.1?
A. 0.1251 B.
0.0107 C. 0.4585 D. 0.9893
55.
For a Normal
Distribution with mean 12 and standard deviation 7.9, what is area to the right
of 30.2?
A. 0.1587 B.
0.9893 C. 0.9356 D. 0.0107
56.
For a Normal
Distribution with mean 5 and standard
deviation 7.6, what is area to the right of 14.1?
A. 0.2743 B.
0.1587 C. 0.1151 D. 0.2301
57.
For a Normal
Distribution with mean -14 and standard deviation 2.8, what is area to the left
of -20.4?
A. 0.0107 B.
0.8235 C. 0.0214 D. 0.0971
58.
For a Normal
Distribution with mean -2 and standard deviation 3.8, what is area to the left
of 2.9?
A. 0.7007 B.
0.9032 C. 0.1936 D. 0.2578
59.
For a Normal
Distribution with mean 4 and standard
deviation 7.1, what is area to the left of 13.2?
A. 0.9032 B.
0.1936 C. 0.2866 D. 0.1587
60.
For a Normal
Distribution with mean -11 and standard deviation 5.0, what is area to the left
of 0.5?
A. 0.1251 B.
0.1587 C. 0.0214 D. 0.9893
61.
For a Normal
Distribution with mean -7 and standard deviation 5.1, what is area in both
tails farther from the mean than -1.9?
A. 0.3173 B.
0.0849 C. 0.6346 D. 0.9151
62.
For a Normal Distribution
with mean 13 and standard deviation 3.5, what is area in both tails farther
from the mean than 7.8?
A. 0.2672 B.
0.1336 C. 0.1587 D. 0.7734
63.
For a Normal
Distribution with mean 10 and standard deviation 5.9, what is area in both
tails farther from the mean than 11.2?
A. 0.8415 B.
0.4602 C. 0.1587 D. 0.5793
64.
For a Normal
Distribution with mean 1 and standard
deviation 7.8, what is area in both tails farther from the mean than 18.2?
A. 0.0278 B.
0.9861 C. 0.1587 D. 0.1357
65.
For a Normal
Distribution with mean -5 and standard deviation 1.6, what value leaves
probability 0.794 in the left tail?
A. NaN B. 0.2060 C. -3.6874 D. 0.8204
66.
For a Normal
Distribution with mean -7 and standard deviation 6.5, what value leaves
probability 0.689 in the left tail?
A. -3.7954 B.
-5.3977 C. -10.2046 D. 0.4930
67.
For a Normal
Distribution with mean 12 and standard deviation 1.5, what value leaves
probability 0.825 in the left tail?
A. 0.1750 B.
13.4019 C. 8.9346 D. 0.9346
68.
For a Normal
Distribution with mean -12 and standard deviation 9.6, what value leaves
probability 0.006 in the left tail?
A. -2.5121 B.
12.1166 C. -33.6684 D. -36.1166
69.
For a Normal
Distribution with mean -2 and standard deviation 9.1, what value leaves
probability 0.182 in the right tail?
A. 0.9078 B.
6.2607 C. -1.1275 D. 0.8180
70.
For a Normal
Distribution with mean 0 and standard
deviation 4.0, what value leaves probability 0.077 in the right tail?
A. -4.0777 B.
-5.7022 C. 1.4255 D. 5.7022
71.
For a Normal
Distribution with mean 13 and standard deviation 4.9, what value leaves
probability 0.489 in the right tail?
A. 13.1351 B.
0.0276 C. 12.9324 D. 12.8649
72.
For a Normal
Distribution with mean -3 and standard deviation 1.0, what value leaves
probability 0.133 in the right tail?
A. 1.1123 B.
-3.6250 C. -4.1123 D. -1.8877