Basic Background Knowledge: Review of Economics especially for SUS students 2.      Firms Economics of the Environment and Natural Resources/ Economics of Sustainability K Foster, CCNY, Spring 2012

 

1.       Firms Choosing How to Produce

Assume that firms want to maximize profit, p, which is Revenue minus Cost.  This is far from a perfect description of the world of course but it's a start.

 

Split the production decision into two parts: first, if a firm wants to make a particular quantity of output, what is the cheapest way to make it; second, how much output will a firm choose to make.  This division allows us to focus on particular pieces first.

 

The first question – to make a particular quantity of output, what is the cheapest way to make it? – gives us the single essential number: the cost of that amount of output.   The cost of this output is the only important item that the firm, when choosing amount of output to produce, needs to know.  It does not need to know the quantities of inputs or relative costs.  This split can also be thought of as reflecting a firm's organization: there is the corporate level that makes the decisions about how much product to make, if those output levels have a particular cost.  Then these decisions are communicated to the plants that make the output, where each plant manager is told to make a particular amount of output, using the cheapest input mix possible.  The plant manager doesn't need to know how a particular quantity of output was chosen; the corporate level doesn't need to know details of how that output is made, just the cost.

 

At this level we are not paying attention to questions of corporate structure.  Given the decision structure from above, we might think of the plant managers as being a separate firm, outsourcing production.  (A brand-name computer maker buys chips from a separate company; it doesn't need to know details of how the chips are made, indeed that might be a close-held secret.  All it needs to know is the cost.)  Our modern economy has many such firms providing corporate services, from high-level research down to the company cafeteria.  The informational savings are immense: a firm doesn't need to know the details of how each input is made, it just needs to know how much they cost.  If they want paper, they don't need to ask about how many trees grew for how long, they just need the cost per ream.  (This is why central planning fails, since there are no prices and so no informational savings.)

 

We begin our analysis at the base, at the level of the plant, which is given an order for a particular quantity of output and must choose how to most cheaply make it.  Again we divide the decision into two parts: first asking what is physically possible (what inputs can make the output) and then asking which combination is cheapest.

 

2.      One Input

The simplest case is where one input makes one output, so we simply have .  The marginal product of the input is how much additional output is made by adding more input, or , which is the slope of the graph.  Assume that it is increasing, continuous and convex.

 

The assumption of  being an increasing function (i.e. that  ) is anodyne.  Just as with utility, if output actually falls when inputs rise then you don't need an advanced degree to figure out that you should cut back.  The interesting problem occurs when output could still be increased and you want to figure out if it is profitable.

 

 

 

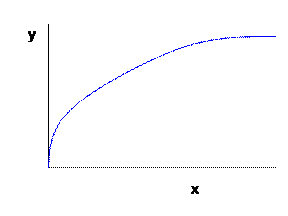
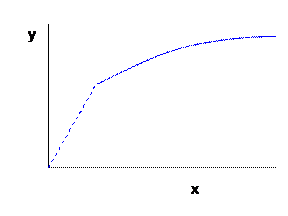
The assumptions of continuity and convexity don't seem as obvious.  But they can be solved if we think of the firm's problem over a slightly longer period.  Suppose that a firm's underlying physical process of production is discontinuous: it takes at least 100 units of input in a day to make 100 output units, but less than 100 of the input just won't even start up the machine.  Is the firm's production function to be considered discontinuous?  Well what if the firm got orders for 50 units of output per day – what would it do?  Clearly it could just run the machine every other day, and average 50 units of output with 50 units of input per day.  If orders run at 80 per day then the machine is run on 4 out of 5 days, and so forth.  Of course this assumes that the output is storable and that the time over which we are speaking is relatively short (more on this later).  But the assumption is not too bad.

 

The convexity assumption comes by the same assumption.  If the firm can make 100 output with 100 input then it could make at least half as much output with half the input.  (On the graph, any chord drawn between 2 points will lie on or beneath the production function.)  If there were non-convexities in the underlying physical process then, again, production could be structured to avoid these.

 

 

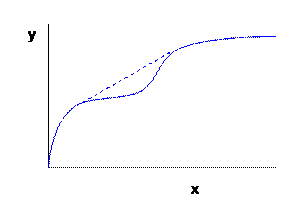
The convexity assumption is also why we often talk about a "Law" of Diminishing Marginal Product.  It is reasonable to assume that the Marginal Product, , is diminishing (or at least not increasing) because if it were increasing then, as in the graph above, the firm would want to figure out ways to exploit this.

 

Clearly, assuming just one input to the production function is restrictive.  I can't think of too many things that are produced in that way (except for the world's oldest profession).  We want to consider multiple inputs.

 

3.       More than One Input

We commonly limit ourselves to two inputs because that allows easy graphing and still gets to most of the complexities.  But you should be able to see how the number of inputs could be increased. 

 

Now describe the production plant with a production function where inputs  are transformed into outputs by way of a production function: .  We could imagine a wide variety of production functions but we assume that it has some basic properties.  Note that, whereas in the consumer problem, we were reluctant to make restrictions directly to the utility function and instead discussed assumptions about the underlying preferences, that was because utility was un-measurable and only a convenient descriptive device.  Production is more easily measured as long as there is some physical output: tons of steel or pairs of sneakers or casks of beer.  So we make assumptions directly about the production function.

 

We again assume that the production function is increasing (so more inputs lead to more output), continuous, and convex (or something like convex).  Now define each input's Marginal Product: , where we use the function notation to remind ourselves that the MP for each input is likely to be different, for different levels of each input.  This is important – there are likely to be complementarities in production.  The Marginal Product of one input is likely to depend on the levels of other inputs as well.  (For example we often hear statistics that workers in third-world countries are not as productive as US workers – this doesn't mean they're any worse, just that they have different levels of other inputs.)

 

Again we assume diminishing marginal products, that  falls as input 1 rises (holding constant input 2) and vice versa.  This "holding constant" part is particularly important since, while in the long run we might be able to increase output by increasing both inputs, in the short run one input or the other is usually less flexible.  Consider the typical office worker nowadays, who usually gets one computer.  If a company hires more people without buying more computers, then the productivity of the new people (whatever their talent!) will be limited as they have to jostle for computer time.  Similarly if the company got new computers without hiring new people – a few people might get multiple computers on their desks, and some might be more productive with those new computers, but not very much.

 

This is distinct from returns to scale, which asks what happens to output if all of the inputs are increased.  Hiring people without getting more computers might not raise output much; getting computers without hiring more people might not raise output much; but hiring more workers and giving each a computer might still raise output.  Diminishing Marginal Products for each input alone does not imply diminishing returns to scale.

 

To more formally define returns to scale, suppose a firm doubled its inputs, and ask what would happen to outputs?  If output doubled exactly then a firm would have constant returns to scale (CRS).  If output increased by more than double then the firm has increasing returns to scale (IRS).  If output increased by less than double then there are decreasing returns to scale (DRS).  To put this a bit more abstractly, we compare the output from doubling the inputs, , with twice the original output, .  If  then production is CRS; if  then IRS; if  then DRS.  Or, more generally, for any scale factor , if  then production is CRS; if  then IRS; if  then DRS.

 

Short Run vs Long Run

Often one input is more flexible than the other.  This means that our analysis should distinguish between the short run (when one input is fixed) and the long run (when both inputs are flexible).  Often we assume that labor is flexible and capital (the machines) are fixed since building, say, a new assembly line takes time.  But other firms might have different rankings – universities have tenured faculty, many of whom have been there longer than some of the buildings on campus!

 

4.      Profit Maximization

A firm's profits are revenues minus costs, so a firm selling n different output goods, each for price p_i, and using m different inputs, each with cost w_j, would have profit .

 

First note that the costs must all be put into the same units – dollars per time unit.  Which raises the question, if a firm buys, say, a truck that is expected to last for 5 years, how is this cost compared against the daily wage of the person driving it?  To answer this we suppose that another company were set up that just rented out trucks: it goes to the bank, gets a loan to buy the truck, and then charges enough per day to pay off the loan per day.  We consider that, even if a company doesn't actually rent the truck but actually buys it, that it could have rented the truck.  So the rental rate is the correct cost of that capital good.  In the real world more and more companies are separating their daily operations from their loan portfolio and renting equipment.  If you work at an office, you know that most photocopiers are rented.  Airlines rarely own their own jets, they rent them.  Offices are usually rented space.  (Employees are rented, too!)

 

The companies have figured out that correctly measuring costs allows them to make better decisions.  Capital goods which are owned and given away internally as if they had zero cost are not efficiently used.

 

Economists also measure costs differently from the way that accountants do regarding payments to shareholders/owners.  If a public company has an IPO and sells its shares for $100 each, then those shareholders expect something in return.  They expect that the dividends (and/or capital gains) will return them as much or more money as if they had invested their $100 in some other venture.  So the company had better return $8 per year if the investors could have gotten 8% returns.  An accountant would count this $8 per share as a "profit" but economists see that as a cost to be paid to shareholders for the use of their money (their capital).  If the firm were to return just $6 then the shareholders would be angry and the firm would be in trouble; if the firm returns $12 then the shareholders are delighted.

 

So economists often talk about "zero profits" being a general case, which makes people wonder how much economists know about the real world since any business newspaper daily reports companies making "profits".  But we're just counting different things.  If the regular return to capital is 8% then, if the firm makes $8 that the accountants call profit, we call it a cost and report that the firm made zero economic profit.

 

5.      Profit Maximization with One Input

This means                                                                              

 subject to .  Hiring one more unit of input will raise the firm’s cost by ; this one additional unit of input will raise output by  and so revenues will rise (assuming no market power) by , which is the value of the marginal product.  If  then the firm should hire more inputs; if  then the firm should hire fewer inputs; so in equilibrium .

 

 

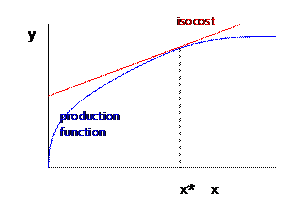
Note that, if one input is fixed, then even the two-input model becomes, in the short run, just this problem of profit maximization with one input.

 

6.      Profit Maximization with Multiple Inputs

Now the firm is to  subject to .  Again the same logic applies.  Hiring one more unit of input one will raise the firm’s costs by  and raise revenues by  so in equilibrium  and .  Also these imply that our usual bang-for-the-buck marginal conditions apply, that  which is the tangent condition that the slope of the isocost equals the slope of the isoquant at optimum.  This condition gives the long-run profit maximizing combination of inputs to be used, which allows us to derive the long-run cost function.

 

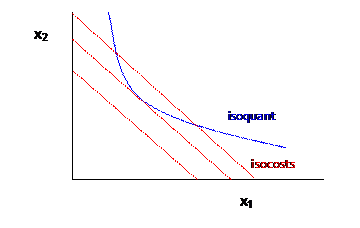
To make a particular amount of output, in the long run the firm minimizes cost by choosing to produce with the inputs set at the tangency.

 

Cost Minimization/Profit Maximization

The firm’s problem to maximize profits generates a dual (sometimes easier) problem, which is how to minimize costs subject to a constraint of making a particular amount of output.  (The constraint is important, though -- if the firm wanted to minimize costs without that constraint, clearly setting y=0 would be best!)

 

If the firm wanted only to maximize revenue (or if the input were costless) then the firm would  subject to .  A "costless" input sounds crazy but remember that Mankiw says, "rational people make decisions on the margin."  Zero marginal cost is not that unusual: it's the usual condition for media companies – they pay a big fixed cost (to record a song or make a movie or TV show), but then their marginal costs are about zero: one more iTunes download does not cost them much! 

 

7.       Marginal Revenue

To figure out this problem of zero marginal cost but changing revenue, we just need another definition.  Marginal Revenue, MR, is the change in revenue per change in output, .  If price is a function of the level of output (e.g. the firm has monopoly power) then MR can be a complex function.  If the firm operates in a competitive market then the price is outside its control, so the increase in revenue from selling one more unit of output is the price, p.

 

But many firms have monopoly power.  Consider a fashion label selling handbags.  They want to sell more because that means more revenue.  But they also know that scarcity has value: some designers sell in only a few select boutiques and can charge very high prices; other designers sell bulk quantities in department stores and cannot charge high prices.  This is a very general problem.

 

A firm that wanted just to maximize revenue would expand production as long as MR>0 and only stop when MR=0, when producing more output would no longer raise its Revenue.

 

Most firms, however, do not simply care about maximizing revenue; they want to maximize profits.  (Particular parts of firms, however, might want to maximize revenue: for instance, most sales people are paid commissions on the sales they generate not necessarily the profits.  Countrywide got paid per mortgage regardless of quality.)

 

A firm that wants to maximize profits will also have to take account of Marginal Cost.  It is also convenient to figure other cost definitions.

 

In a perfectly competitive environment the firm's demand curve is a horizontal line – the market price for this homogenous commodity.  The firm can sell as much quantity as it can produce at that price.  Lowering the price will not increase the amount sold; raising the price will stop all sales.  This is an extreme assumption but, as you think about it, not completely unrealistic.  One of the important points of any business plan for a new company is 'the competition' – what other firms sell and at what price.  If my firm offers the same product then I can't charge a higher price.  Of course my firm might charge a higher price and offer a better product, but this means that I'm selling a different output.

 

The business press sometimes discusses the "commodification" of different markets: for example at one point, when computers were new, the chips were quite different and there were many different prices; now that chips are standardized there is much less variability in price.  Financial markets are commodity markets: nobody offers a "20% sale" on stocks or bonds!  Markets are organized in order to standardize and "commoditize" certain products: e.g. the CBOT offers corn futures to deliver "5000 bushels of No. 2 yellow corn"; or "100 troy ounces of refined gold not less than .995 fineness cast as one bar or 3 one-kilogram bars"; the NYMEX trades gasoline "reformulated gasoline blendstock for oxygen blending (RBOB) futures contract trade in units of 42,000 gallons (1,000 barrels)" for delivery in New York.

 

This is not to say that the market demand curve is flat, just that the curve for the particular firm is flat.  Another way of thinking of it is that the firm is such a tiny player in the whole market that it sees just a tiny piece of it, which is essentially flat.  But even if there are a limited number of companies then a firm might still face a flat demand curve for its product based on the other's price.  A final example: whatever I sell nowadays, I have to know what Amazon or eBay charges for it – most all of my customers will!